Экспериментальная проверка законов динамики поступательного и вращательного движения, соотношения кинематики равномерного и равноускоренного движения, страница 2

где Т₁ и Т₂ - силы натяжения, создаваемые грузами 1 и 2 соответственно; R и J - радиус и момент инерции блока; М_тр - момент силы трения, действующей на ось блока.

Ускорения грузов а₁ = а₂ = а, так как нить считается нерастяжимой. Пренебрегая проскальзыванием нити по блоку, можно положить

Решив систему уравнений относительно ускорения а, получим

                           (3)

Если допустить, что силы трения в блоке пренебрежимо малы по сравнению с mg, то М_тр/R<< mg. Если, далее, пренебречь массой блока, от которой зависит момент инерции J, то J/R²<< 2M + m. Тогда

Если, наконец, масса перегруза значительно меньше масс грузов (m << 2M), то ускорение можно рассматривать как линейную функцию массы перегруза:

a = mg/(2M).                             (4)

Порядок выполнения работы

Задание 1. Проверить зависимость ускорения от массы перегруза. Для этого определить ускорение груза 2 с перегрузами разной массы и построить график функции a(m). Если его вид будет соответствовать теоретической зависимости (4), это подтвердит справедливость законов механики, на основании которых получено соотношение (3).

Задание 2.Экспериментально определить значения момента инерции блока J и силы трения в блоке F_тр. Полученные данные позволят подтвердить правильность сделанных упрощающих предположений, приводящих от уравнения (3) к уравнению (4).

Чтобы найти значение F_тр, следует определить сначала момент силы М_тр. Для этого запишем выражение (3), содержащее неизвестные J и М_тр, для двух пар значений а и m:

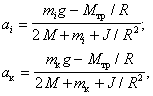
где i и к - индексы, обозначающие порядковый номер измерения.

Решив эту систему относительно J и М_тр , получим

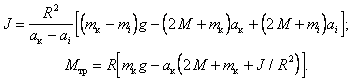                       (5)

Сила трения

F_тр = M_тр/r ,                                        (6)

где r - радиус оси блока.

Для выполнения заданий нужно знать ускорение грузов на участке 1 (рис.1). Пусть длины участков 1 и 2 соответственно l₁ и l₂ , а t - время прохождения грузом 2 пути l₂. Тогда, согласно уравнению (2), на участке 1 груз 2 приобретает скорость v² = 2al₁, а на участке 2 движется равномерно: l₂ = vt. Следовательно,

                               (7)

Результатом экспериментальной части работы должны стать значения времени t прохождения грузом 2 с перегрузами m пути l₂.

К установке Атвуда прилагается набор из трех колец массами m₁ = 6,50 г, m₂ = 8,80 г, m₃ = 12,60 г. Погрешности масс колец Используя данный набор колец, можно получить восемь различных масс перегруза: m₁,m₂, m₃,  m₁ + m₂, m₁ + m₃, m₂ + m₃  и  m₁ +m₂ + m₃.