



Розв’язання задач математичної олімпіади 2008 р.
1. Знайти всі пари цілих чисел, сума яких дорівнює їх добутку.
Розв’язання: Завдання зводиться до відшукання цілих рішень рівняння
x+y=xy
Після простих перетворень знайдемо:
(x–1)(y–1)=1, звідки маємо: x–1=–1, y–1=–1 або x–1=1, y–1=1, тобто x=0, y=0 або x=2, y=2.
Відповідь: (0;0), (2;2).
2. При яких цілих значеннях n число
n(n+1)( n+2) поділяється на 24?
Розв’язання: Нехай
n(n+1)( n+2):24. (1)
Так як дане число при будь-якому цілому n поділяється на 3, то (1) буде виконано, якщо
n(n+1)( n+2):8. (2)
Розіб’ємо множину цілих чисел на дві підмножини: множину парних і множину непарних чисел.
1) Якщо n – число парне (n=2х), то і n+2 – число парне. А з двох сусідніх парних чисел одне обов'язково ділиться на 4. Отже, число
n(n+2)
у випадку n – парного буде поділятися на 8.
2) Якщо n непарне, то і n+2 – непарне, а число n+1 – парне. Співвідношення (2) буде виконано, якщо
n+1:8, тобто n+1=8m, звідки n=8m-1.
Відповідь: 2k або 8m–1 (k, m – цілі числа).
3. Розв’язати систему рівнянь
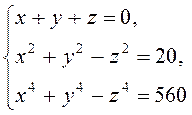
З першого рівняння
z= –(x+y). (1)
Підставляючи у друге рівняння, одержимо –2xy=20
xy=–10 (2)
З другого рівняння x2+y2=z2+20.
Піднесемо обидві частини до квадрату, одержимо x4+2x2y2+y4=z4+40z2+400.
Підставляючи в це співвідношення замість x4+ y4– z4 число 560, а замість 2x2y2 число 200, одержимо: 40z2=360; z=±3. Враховуючи (1) і (2), одержимо дві системи рівнянь
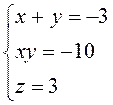 і
і 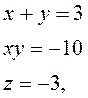
розв’язуючи які, знайдемо
|
1) |
x1=2, |
2) |
x2=-5, |
3) |
x3=5, |
4) |
x4=-2, |
|
y1=-5, |
y2=2, |
y3=-2 |
y4=5, |
||||
|
z1=3, |
z2=3 |
z3=-3 |
z4=-3. |
4. Група студентів складала іспит з математики. Число студентів, які успішно склали екзамен, міститься в інтервалі від 96,8% до 97,6%. Яка найменша можлива кількість студентів у групі?
Розв’язання.
Якщо число студентів, які здали екзамен, міститься в інтервалі від 96,8% до 97,6%, то кількість студентів, які екзамен «завалили», міститься в інтервалі від 2,4% до 3,2%.
Якщо в групі було n
студентів, а невдача спіткала х студентів, то ![]()
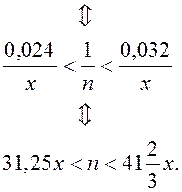
В задачі запитують, яка найменша можлива кількість студентів у групі, тобто яке найменше натуральне n задовольняє останній нерівності.
Ліва межа інтервалу буде найменшою, якщо х найменше, тобто якщо в групі виявиться лише 1 невдаха. Тоді нерівність набуде вигляду:
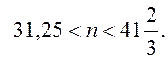
Зрозуміло, що найменше натуральне n, що задовольняє цій нерівності, 32.
Відповідь: у групі 32 студента.
5. Знайти всі функції ![]() , які при будь-яких дійсних x,y задовольняють рівняння
, які при будь-яких дійсних x,y задовольняють рівняння
![]() .
.
Розв’язання .
Якщо у функціональне рівняння підставити ![]() , то дістанемо рівняння
, то дістанемо рівняння ![]() або
або ![]() . Покладаючи в цьому рівнянні
. Покладаючи в цьому рівнянні ![]() , дістаємо
, дістаємо ![]() , тобто
, тобто 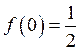 . Отже,
. Отже, 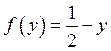 , тобто
, тобто 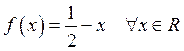 .
.
Перевірка показує, що функція 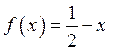 задовольняє умову задачі.
задовольняє умову задачі.
Відповідь: 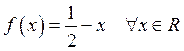 .
.
6. Обчислити А2008, де 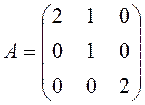 .
.
Розв’язання:
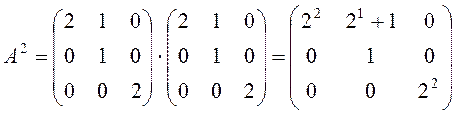 .
.
Покажемо за методом математичної індукції, що
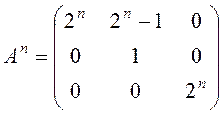 .
.
Нехай це виконується. Покажемо, що даний факт має місце і при n+1:
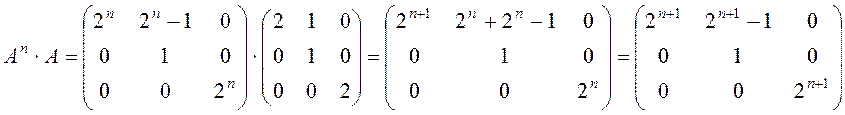
Відповідь: 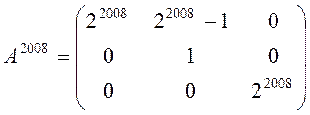 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.