Решение системы линейных алгебраических уравнений методом Крамера и с помощью обратной матрицы

Отчёт по лабораторной работе №11

            Тема. Решение системы линейных алгебраических уравнений

Задание. Решить СЛАУ двумя способами: методом Крамера и с помощью обратной матрицы. Сделать проверку.      

            Решение.

            Пусть система линейных уравнений имеет вид

1,8х₁    -0,2х₂  0,1х₃=0,4

-0,1х₁  1,8х₂    -0,1х₃=0,8

-0,3х₁  0,2х₂    -0,2х₃=0,2

Введём обозначения: А=-матрица коэффициентов системы

Х=-вектор неизвестных, В=-вектор свободных членов.

Матрица коэффициентов системы получается в результате сложения матриц D и kC, где k- параметр, изменяющийся по некоторому закону ( в данном случае равен 7).

Матрицы для нахождения коэффициентов СЛАУ:

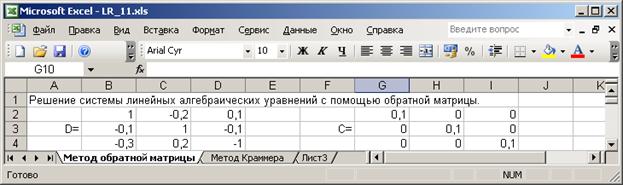
Матрица коэффициентов системы, полученная в результате расчётов:

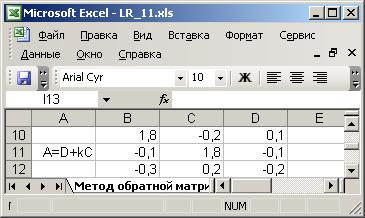
Расчёт выполнен по формуле: =B2:D4+E7*G2:I4

Вектор свободных членов:

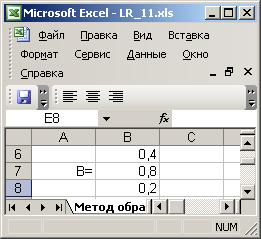
 Решение системы с помощью обратной матрицы

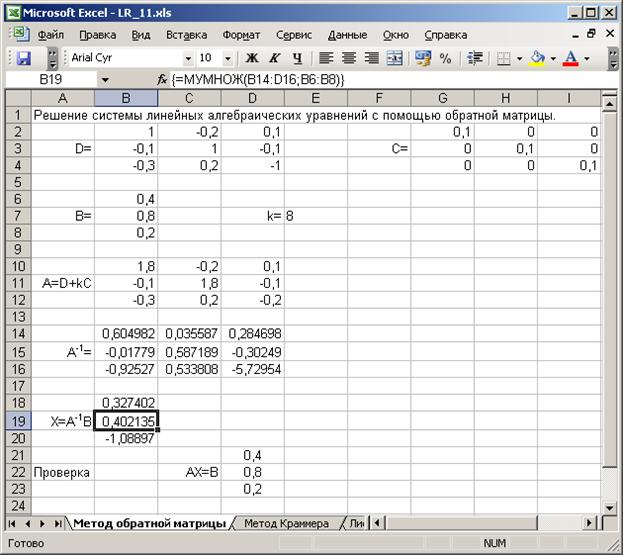
Примеры вычислений:

            Для нахождения обратной мтрицы выделяем интервал ячеек 3х3: В14:D16.

Вводим формулу: =МОБР(B10:D12). Нажимаем Ctrl+Enter+Shift. (Появляются фигурные скобки {}).

Для нахождения вектора неизвестных выделяем интервал ячеек В18:В20 и вводим формулу: =МУМНОЖ(B14:D16;B6:B8). Для завершения ввода нажимаем Ctrl+Enter+Shift.

Выполняем проверку. Находим значения свободного вектора по формуле: =МУМНОЖ(B10:D12;B18:B20).

Решение системы методом Крамера

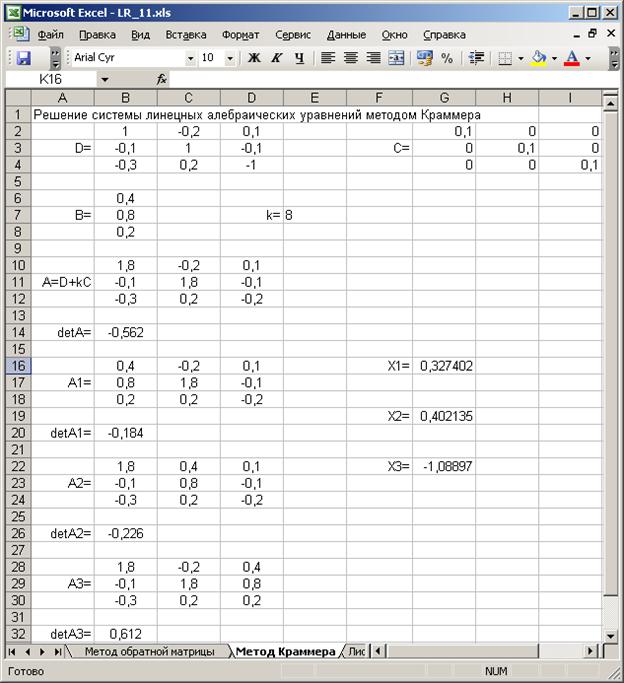
Примеры Используемых формул:

detA: =МОПРЕД(B10:D12)

detA1: =МОПРЕД(B16:D18)

X1=B20/B14