Расчет элементов крепи горной выработки, страница 2

Элемент АВ нагружен распределенной нагрузкой q₁, элемент CD – распределенной нагрузкой q₁, сосредоточенной нагрузкой, равной Р₁ и Р₂. Элементы AC и BD (рис.2, в)     нагружены распределенной нагрузкой

q₃ = q₁ cos α + q₂ sin α , Н/м,

q₃ = 3800 * 0,342 + 1400 * 0,939  = 2299 Н/м,

а также распределенной продольной нагрузкой

q₄ = q₁ sin α – q₂ cos α , Н/м,

q₄ = 3800 * 0,939 – 1400 * 0,342  = 3092Н/м

При равенстве Р₁ = Р₂ = Р расчетная схема обладает симметрией относительно вертикальной оси.

Таким образом, каждый из элементов крепи можно рассматривать как балку на двух опорах (рис.2, а, б). Примем для определенности поперечное сечение всех элементов в виде прямоугольника со сторонами h и b.

Рис. 2.

2.   Построение эпюр поперечных сил и изгибающих моментов

2. 1. Находим реакцию в опорах C и D. Из условий симметрии очевидно, что           R₁ = R₂ = R; Н₁ = Н₂ = Н (рис. 3,а.). Для неподвижных опор C и D из условий равновесия всей системы в целом получим:

Σу = -2Р + 2R + q₁l₂ – q₁l₁ = 0

отсюда:

R = -1/2 [-2P + q₁(l₂ – l₁)] = -0,5*[-2*300000 + 3800*(6,6 – 4,2)] = 295440 Н.

Рис.3.

2.2.  Определяем реакции в шарнирах А и В. Для этого рассмотрим условие равновесия каждого из элементов крепи. Для элемента АВ (рис. 3,б.):

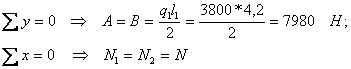
Для элемента BD и АС (рис. 3, в.):

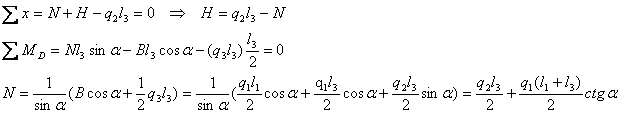
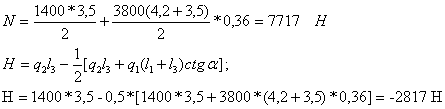
Проекции на нормаль к осевой линии определяются по формулам:

В_n = -B cos α + N sin α = -7980 * 0, 342 + 7717 * 0,939 = 4522 Н

D_n = H sin α + R cos α =-2817*0,939+ 295440*0,342= 98395 Н

Проекции реакции на осевую линию балки вычисляются по формуле:

В₀ = B sin α + N cos α = 7980 * 0,939 + 7717 * 0,342 = 10132 Н

D₀ = -H cos α + R sin α = 2817 * 0,342 + 295440 * 0,939 = 278382 Н

2.3.  Строим эпюры поперечных сил и изгибающих моментов для каждого из элементов крепи, предполагая, что каждый из них находится в состоянии плоского изгиба (осевые усилия не учитываются) и считая все реакции положительными (рис.4). Каждый из элементов крепи представляет собой балку на двух  опорах.

Рис. 4.

3.  Расчет элементов крепи на прочность по наибольшим нормальным

напряжениям.

    1.     Расчет по нормальным напряжениям (плоский изгиб).

Исходя из максимальных изгибающих моментов, действующих в элементах крепи, определим размеры поперечных сечений этих элементов. Из условия  для прямоугольного сечения элемента найдем

4. Построение главных площадок и определение главных напряжений в массиве.

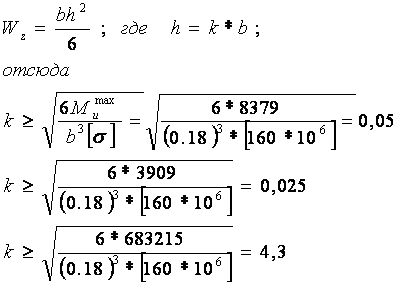
Главные площадки и главные напряжения в элементе крепи. Определим направление главных площадок и величины главных напряжений в глубине массива, т.е. в точках, удаленных от выработки ( вблизи выработки будет существенно сказываться взаимодействие массива и крепи). На грани элементарного куба с ребрами единичной длины будут действовать напряжения, пропорциональные q₁ и q₂ (рис.5, а). Главные напряжения определяют по формуле