Использование Mathcad в качестве суперкалькулятора, страница 2

·  При помощи этой же команды в математическом выражении можно выражать одну переменную через остальные.

·  При решении уравнений в символьном виде, необходимо иметь в виду, что переменные не должны быть определены заранее.

Задание

1. Решить уравнение: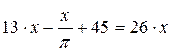

Для решения данного уравнения в численном виде необходимо предварительно задать произвольное значение неизвестной. Для этого при помощи операции присвоения значению х присвоим значение 1.

Затем записываем функцию root после которой в скобках записываем левую часть уравнения (в правой части должен быть ноль) и после запятой указываем искомую неизвестную, после чего ставим знак вычисления «=»

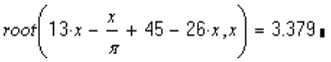
Если корень данного уравнения необходим нам в дальнейших вычислениях, то запись решения удобно осуществлять в следующем виде:

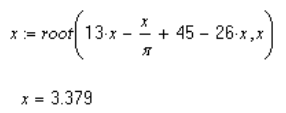
2.  Решить уравнение:

Для поиска всех корней данного уравнения, решение его необходимо осуществлять в символьном  виде (т.к. уравнение имеет более одного корня). Выбрав из панели «символика» команду «solve» в маркере слева от команды записываем левую часть уравнения, в маркере с правой части команды указываем искомую неизвестную.

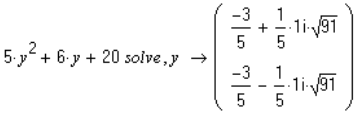
Из результата видно, что поиск решения осуществляется и в комплексных числах.

3.  В уравнении 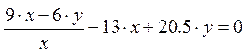 выразить переменную y через переменную x.

Для решения данной задачи используем команду «solve» в маркере слева от команды записываем левую часть уравнения, в маркере с правой части команды указываем переменную которую необходимо выразить, то есть y.

Лабораторная работа №6

решение систем линейных уравнений.

Цель работы: Овладение навыками решения систем линейных уравнений в численном и символьном виде.

Предварительные замечания

·  Численное решение систем линейных уравнений  осуществляется с использованием блока «Given…Find(неизвестная)=».

·  Как и в случае решения уравнений в численном виде, для поиска корней необходимо задать начальную итерацию.

·  Символьное решение систем линейных уравнений  осуществляется с использованием блока «Given…Find(неизвестная) ® »

·  Запись уравнение входящих в систему производиться с использованием команды тождественного равенства «=» из панели «булево».

Задание

1.  Решить систему линейных уравнений:

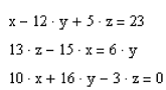
Задаем произвольные значения неизвестных:

Набираем команду «Given» после которой с использованием знака тождественного равенства записываем уравнения входящие в систему.

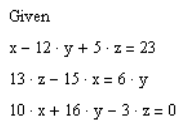
Присваиваем матрице неизвестных команду поиска корней системы уравнений «find(x,y,z)» и находим неизвестные.

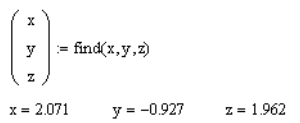
2.  Решить вышеуказанную систему уравнений в символьном виде

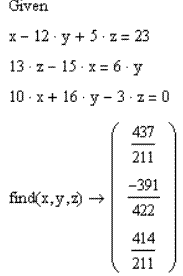
Для решения вместо знака «=» после команды «Find» воспользуемся командой «®» символьного вычисления из панели «символика»

Для того чтобы сейчас определить решение в численном виде, достаточно после символьного результата поставить знак численного вычисления «=».

Лабораторная работа №7

численное решение дифферинциальных уравнений.

Цель работы: Овладение навыками решения дифференциальных уравнений, построения графического отображения решения дифференциальных уравнений.

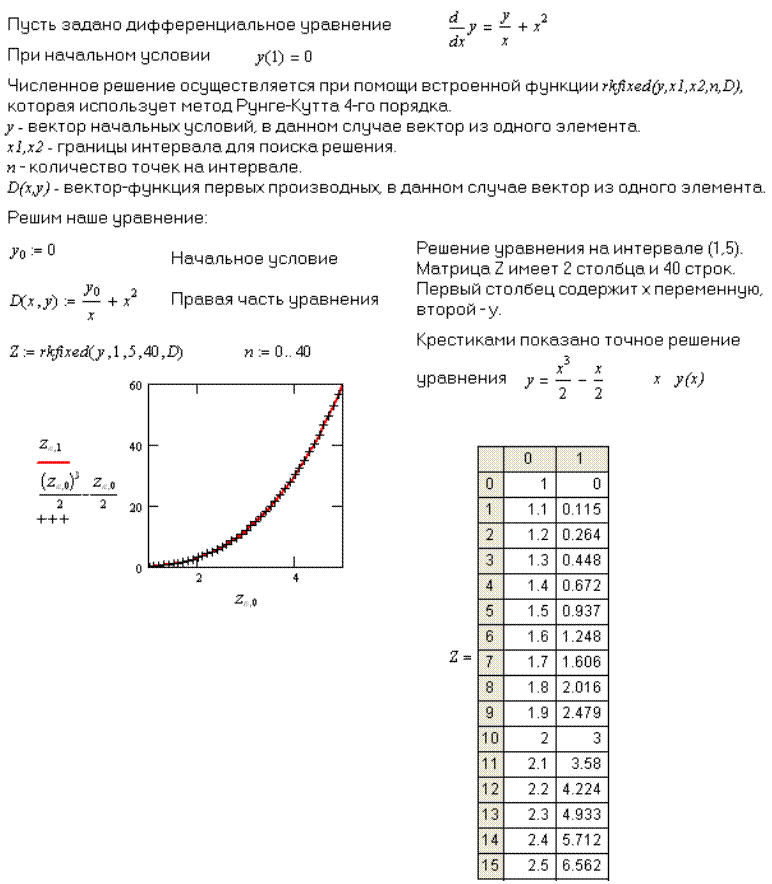
Задания для контрольных занятий

1. Решить уравнения:

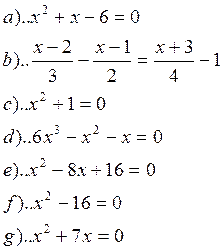
2. Построить линии, заданные уравнениями:           

а) y=cosx               г)  y=                  ж)  y=logx                          к)  y=x

б)  y=x                   д)  y=-2x                 з)  y=

в)  y=          е)                и)  y=2x

3. Определить точки пересечения с осями координат:

а)  4x+y-5=0                г)  y=              ж)  y=sinx

б)  y=2x-3                    д)  2x+3y=0 в)  y=-2x-3                   е)   y=

4. Построить область ограниченную линиями

а)   ,

б)  x + y = 1 , x – y = 1 , x + y = 3 , x – y = -1

в) 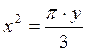 ,  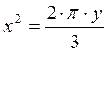, г) y=sin (x),

5. Построить  график   функции    h(x)    от   x  при  условии,  что

h(x)=f(x)     если  f(x)³0

h(x)=10       если  f(x)<0

f(x)º5×sin(x),    x   изменяется   от   -20   до  18   с  шагом  0,2

6. Построить  график   z(k)   от  k   при  условии,  что

z(k)=г(k)     если   r(k)³0

z(k)=200     если   г(k)<0 г(k)º5k+k²,   k   изменяется   от   -20  до  18  с  шагом  0,2

7.  Найти   интеграл:

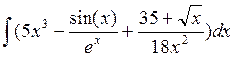
8. Найти:

     `

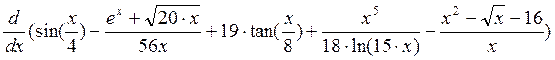9. Найти производную

а) 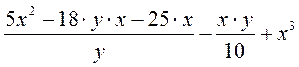 относительно х б) х² + 3х +5, результат расположить на второй строке, не используя знак  ®.

10. Определить интеграл

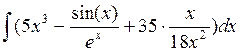
11. Найти

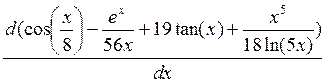
12. Упростить

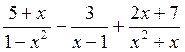
13. Разложить

а)

б) (sin(х) + y)⁴

14. Решить уравнение

cos(2x)-sin(x)=1/2

а). Решить уравнение численно.

б). Решить уравнение символьно.

15. Построить график.     cos(2x)-sin(x)=1/2

оси пересекаются , линия графика прерывистая зеленая.

на этом графике показать линию x=1.

16. Найти точки пересечения с осями x,y графика     cos(2x)-sin(x)=1/2

а) на интервале от –п/2  до п/2 с шагом 0,2 ;  б) на интервале –п/2 до п с шагом 0,3.      в). На этом графике построить линию с координатами y=1 ,x=-5 до 5;

17. Решить систему уравнений

2x₁+x₂+3x₃=8

 

4x₁ +x₂ +2x₃ =5

2x₁ +2x₂ –4x₃ = -9

 

а). Решить систему численно.

б)  Решить систему символьно.

18. Решить систему уравнений

3х₁ + 2х₂ + 3х₃=4

2х₁ + 2х₂ + 6х₃=6

5х₁ + 4х₂ + 3х₃=5

а). Решить систему численно.

б). Решить систему символьно.

19. Решить уравнение относительно переменной х, y

а)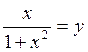

б) (sin(х) + y)⁴

в) tan(x) + cos(y) = 1 + sin(x)

20. Решить задачу

Дан изгибаемый элемент прямоугольного сечения с размерами

b=10 см           h=200 мм

Определить как измениться напряжение в элементе (МПа) при изменении изгибающего момента а) от 50 кН*м до 150 кН*м б) от 1000 кН*см до 10000 кН*см