Проектирование элементов ЭВУ. Синтез конечного автомата Мили, страница 2

Преобразуем таблицу переходов автомата в таблицу возбуждения памяти. Для обеспечения каждого такого прехода из исходного состояния памяти в последующее нужно подать на входы элементов памяти определенные сигналы. Эти сигналы и записываются в таблицу возбуждения памяти. Каждый бит изменнения состояния будет характеризовать состояние выхода отдельного JK-триггера. В соответствии с выше сказанным изобразим таблицу возбуждения памяти (таблица №5).

Таблица №5

X1X2	Q1Q2
	0	0	0	1	1	0	1	1
	J1K1	J2K2	J1K1	J2K2	J1K1	J2K2	J1K1	J2K2
00	0  -	1  -	-  -	-  -	-  -	- -	-  -	- -
01	1  -	1  -	0  -	-  0	-	-  -	-  0	-  0
10	1  -	0  -	0  -	-  1	-  1	0  -	-  0	-  1
11	-  -	-  -	1  -	-  0	-  -	-  -	-  -	-  -

Составим логические уравнения для входных сигналов JK-триггеров. Записывая их «по единицам» получаем СДНФ:

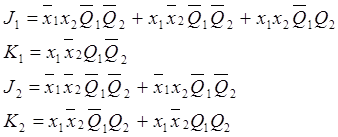
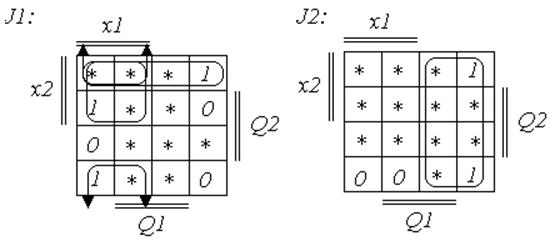
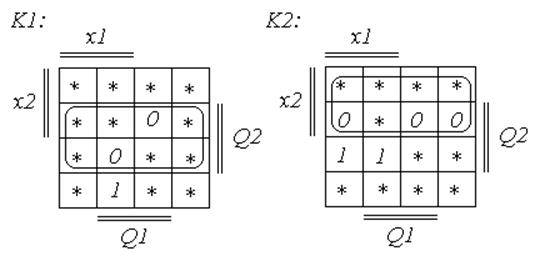
Минимизируем полученные уравнения выходных сигналов у1 и у2, и входных сигналов JK-триггеров при помощи карт Карно. Там, где функции переходов и выходов не определены, доопределим их единицами.

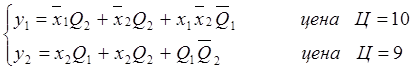
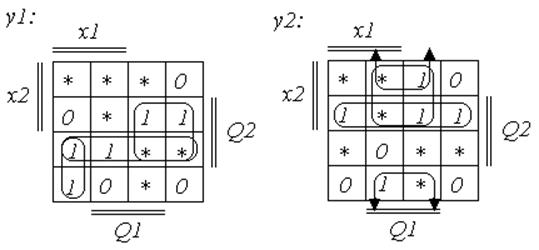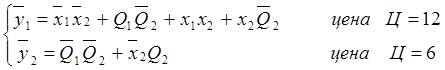
Ориентируясь на цену, предпочтительней будет использовать функции .

Сравнивая цены ФАЛ составленных «по единицам» и «по нулям» можно убедиться, что они равны.

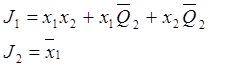
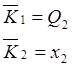
Синтез КА Мили на микросхемах

Рис.3  Принципиальная схема КА автомата Мили

Программная реализация автомата

Преобразование исходного автомата Мили в автомат Мура

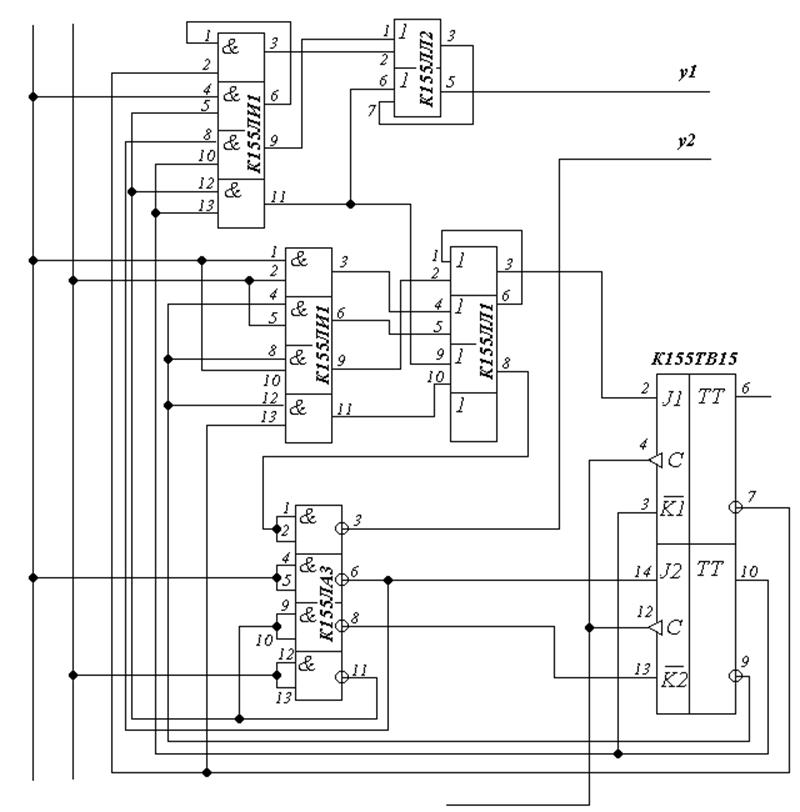Составим совмещенную таблицу переходов автомата Мили (таблица №6).

                                                                                                              Таблица №6

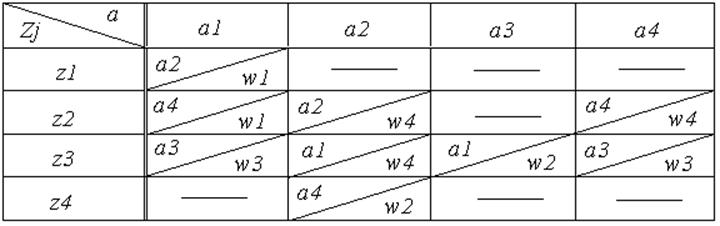Переход к автомату Мура осуществляется в следующем порядке:

1. Находим множества B_s, определяемые числом различных выходных сигналов на дугах, входящих в данное состояние.

2. Составляем таблицу переходов автомата Мура на основании таблицы переходов автомата Мили и состояний B_s  (s=1,2,3,4).

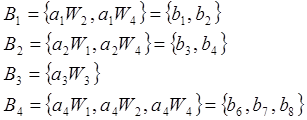
Таблица №7

Zj\bi	b1/W2	b2/W4	b3/W1	b4/W4	b5/W3	b6/W1	b7/W2	b8/W4
Z1	b3	b3	-	-	-	-	-	-
Z2	b6	b6	b4	b4	-	b8	b8	b8
Z3	b5	b5	b2	b2	b1	b5	b5	b5
Z4	-	-	b7	b7	-	-	-	-

Для полученного автомата Мура составим граф (рис. 4).

Рис. 4 Граф автомата Мура

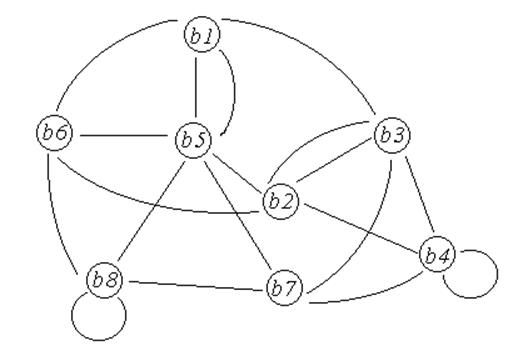Пусть автоматы Мили и Мура находятся в начальных состояних a1 и b2 соответственно. Убедиться в эквивалентности преобразования можно путем подачи на входы исходного автомата Мили и полученного автомата Мура некоторой последовательности букв входного алфавита, например такой:

 при этом выходная последовательность обоих автоматов будет следующей:

, что свидетельствуют об эквивалентности автоматов Мили и Мура.

Составление схемы алгоритма и программы, реализующую автомат Мура на языке ассемблера микропроцессора К580

Процесс программной реализации разбивается на ряд этапов.

1. Определение требуемого числа двоичных разрядов, необходимых для представления кодов внутренних состояний, входных и выходных сигналов:

2. Кодирование автомата и перевод записи таблиц переходов и выходов из символического алфавита в двоичный.

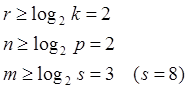
Произведем кодирование автомата.

Таблица №8

zi \ xj	X1	X2	wi \ yj	y1	y2
Z1	0	0	W1	0	0
Z2	0	1	W1	0	1
Z3	1	0	W3	1	0
Z4	1	1	W4	1	1

Таблица №9

	Q1	Q2	Q3
b1	0	0	0
b2	0	0	1
b3	0	1	0
b4	0	1	1
b5	1	0	0
b6	1	0	1
b7	1	1	0
b8	1	1	1

Переводим таблицу переходов (выходов) в двоичный алфавит

Таблица №10

X1X2	Q1Q2Q3/y1y2
	000/01	001/11	010/00	011/11	100/10	101/00	110/01	111/11
00	010	010	-	-	-	-	-	-
01	101	101	011	011	-	111	111	111
10	100	100	001	001	000	100	100	100
11	-	-	110	110	-	-	-	-

3. Обозначим символами Еi внутренние состояния автомата и составим для них «по единицам» логические уравнения.

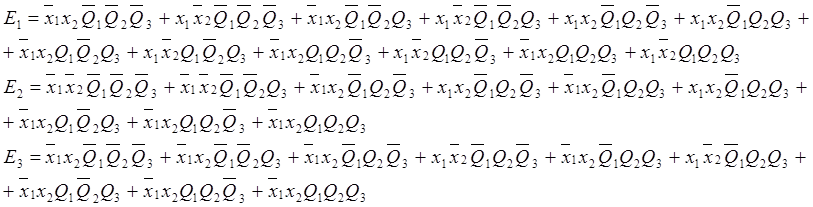
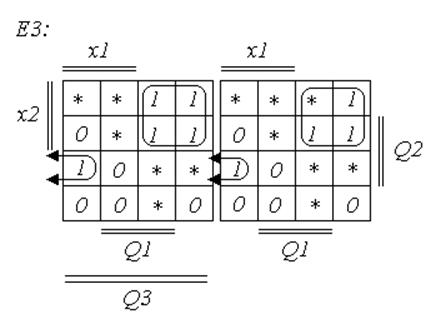
Минимизируем полученные функции Е1, Е2, Е3 картами Карно.

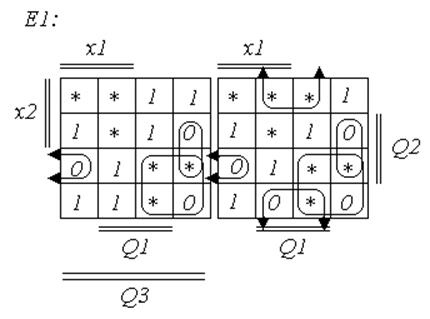Минимизировать данную функцию выгодней «по нулям», в таком случае она примет следующий вид.

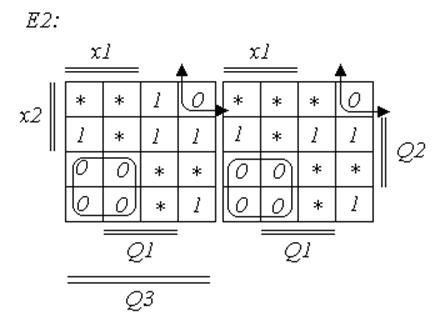Минимизировать данную функцию будем «по нулям».

Таким образом, получаем систему минимизированных уравнений: