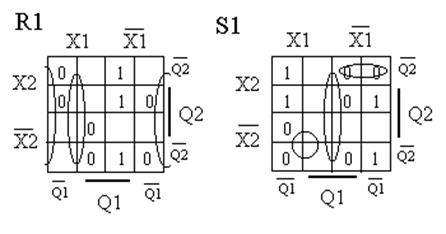
сигналов на каждом информационном входе каждого триггера. Так как функции переходов и выходов не определены на некоторых наборах аргументов, доопределяем карты Карно на этих наборах нулями c целью проведения контуров наиболее высокого ранга. Так, для R1 , S1 R2 S2 карты Карно имеют следующий вид:
 |
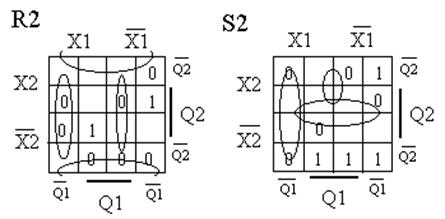 |
Рис.5. Карты Карно для R1 S1 и R2 S2.
Записывая их "по нулям", получаем СДНФ:
![]()
![]()
![]()
![]()
Д: Синтез комбинационной части конечного автомата.
Для синтеза конечного автомата несколько перепишем полученные ФАЛ для сигналов возбуждения памяти:
![]() (Ц=1)
(Ц=1)
![]() (Ц=2)
(Ц=2)
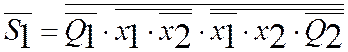 (Ц=5)
(Ц=5) ![]() (Ц=3)
(Ц=3)
Где ![]() (Ц=1)
(Ц=1)
Общая цена получилась=12
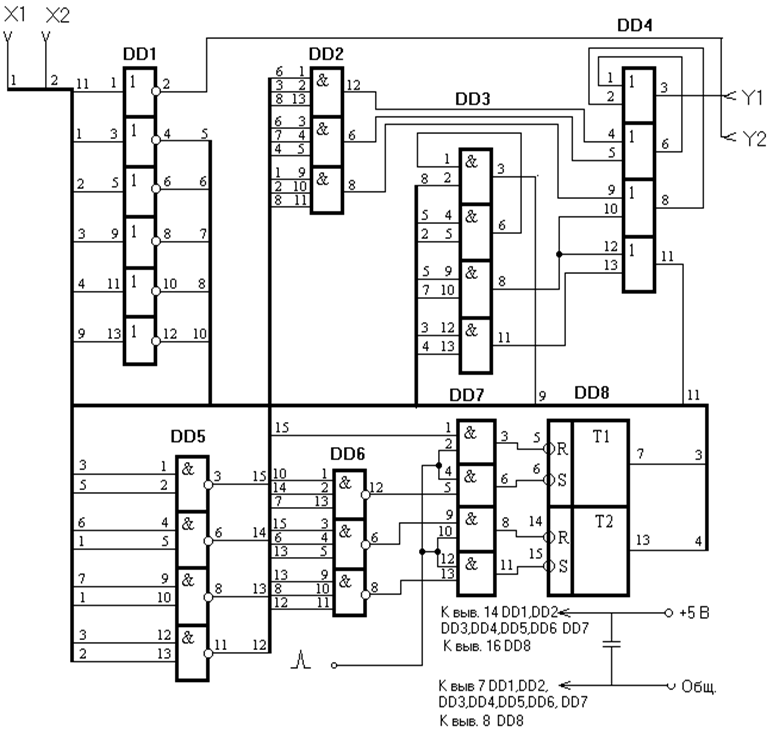
По полученным минимальным формам составляем логическую схему комбинационной части автомата на микросхемах выбранной серии. Приведем схему автомата (Приложение 1).
Приложение 1
Приложение 2
Позиционное обозначение в схеме |
Номинал |
DD1 |
К555ЛН1 |
|
DD2 |
К555ЛИ3 |
|
DD3 |
К555ЛИ1 |
|
DD4 |
К555ЛЛ1 |
|
DD5 |
К555ЛА3 |
|
DD6 |
К555ЛА4 |
|
DD7 |
К555ЛИ1 |
|
DD8 |
К555ТР2 |
|
C1 |
0,47 мкФ + 10% |
2.Программная реализация автомата
A: Преобразование исходного автомата Мили в автомат Мура.
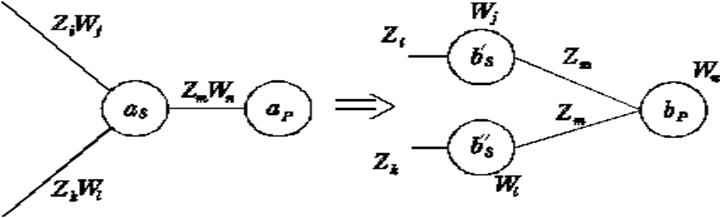 |
автомат Милиавтомат Мура
Рис.6 Переход автомата Мили в автомат Мура.
Пусть задан автомат Мили совмещенной таблицей переходов, которой соответствует граф, изображенный на рис.3.
|
|
|
|
|
|
|
|
|
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
Имеем: ![]()
Переход к автомату Мура осуществляется в следующем порядке:
1.
Находим множества ![]() , определяемые числом
различных выходных сигналов на дугах, входящих в данное состояние (см. рис.3).
, определяемые числом
различных выходных сигналов на дугах, входящих в данное состояние (см. рис.3).
![]()
![]()
![]()
![]()
2. Составляем таблицу переходов
автомата Мура на основании таблицы переходов автомата Мили и состояний ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
|
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
- |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для полученного
автомата Мура несложно составить граф, понимая, что его выходные сигналы ![]() определяются
внутренними состояниями
определяются
внутренними состояниями ![]() . Этот граф изображен
на рис.7.
. Этот граф изображен
на рис.7.
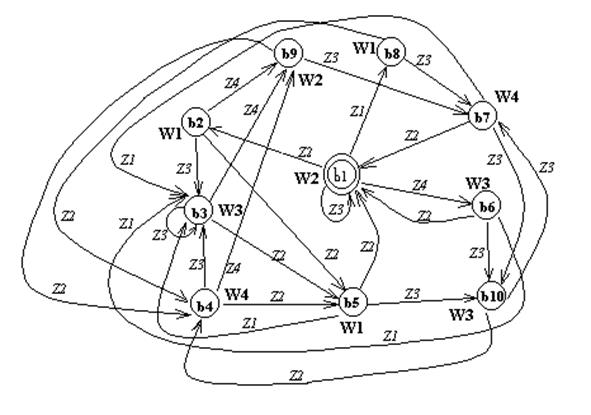 |
Рис.7. Граф автомата Мура эквивалентного автомату Мили
Пусть автоматы Мили и Мура
находятся в начальных состояниях ![]() и b1
соответственно. Убедиться в эквивалентности преобразования можно путем подачи
на входы исходного автомата Мили и полученного автомата Мура последовательности
букв входного алфавита, например такой:
и b1
соответственно. Убедиться в эквивалентности преобразования можно путем подачи
на входы исходного автомата Мили и полученного автомата Мура последовательности
букв входного алфавита, например такой:
![]() при этом выходная последовательность обоих
автоматов будет следующей:
при этом выходная последовательность обоих
автоматов будет следующей:
![]() .
.
Значит, абстрактные автоматы Мили и Мура эквивалентны. При этом выходной алфавит автомата Мура может отличаться от выходного алфавита автомата Мили, поскольку количество внутренних состояний автоматов различно. На этапе структурного синтеза это приводит к тому, что кодировка выходных сигналов также отличается.
В случае необходимости работать в том же выходном алфавите (в кодах исходного автомата Мили) автомат Мура следует дополнить комбинационной схемой – преобразователем кодов, подключаемой к выходам элементов памяти автомата. Выполним это при програмной реализации.
Б: Програмная реализация автомата Мура.
Программа, моделирующая работу автомата Мура, должна реализовывать алгоритм его работы в соответствии с уравнениями:
![]()
![]()
1. Определим требемое число двоичных разрядов, необходимое для представления кодов внутренних состояний, входных и выходных сигналов:
![]() - число
внутренних состояний (
- число
внутренних состояний (![]() );
);
![]() - число
входных сигналов (
- число
входных сигналов (![]() );
);
![]() - число
выходных сигналов (
- число
выходных сигналов (![]() ).
).
Находим:
![]() ;
;
![]() ;
;
![]() .
.
2.Кодируем автомат, переводя запись таблиц переходов и выходов из символического алфавита в двоичный.
Входные сигналы Выходные сигналы
|
Состояние входа |
Биты кода |
Состояние выхода |
Биты кода |
|||
|
|
|
|
|
|||
|
|
0 |
0 |
|
1 |
0 |
|
|
|
0 |
1 |
|
0 |
1 |
|
|
|
1 |
0 |
|
1 |
1 |
|
|
|
1 |
1 |
|
0 |
0 |
|
|
Внутреннее состояние |
Биты кода |
Биты кода |
Выходной сигнал автомата Мили |
||||
|
|
|
|
|
|
|
||
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
1 |
1 |
0 |
0 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|
|
|
0 |
1 |
1 |
0 |
1 |
0 |
|
3.Переводим таблицу переходов(выходов) в двоичный алфавит
|
|
|
|||||||||
|
0001/01 |
0011/00 |
0000/10 |
0010/11 |
0100/00 |
1100/10 |
1000/11 |
0101/00 |
1001/01 |
0110/10 |
|
|
00 |
0101 |
- |
- |
- |
0000 |
0000 |
0000 |
- |
- |
- |
|
01 |
0011 |
0100 |
0100 |
0100 |
0001 |
0001 |
0001 |
0010 |
0010 |
0010 |
|
10 |
0001 |
0000 |
0000 |
0000 |
0110 |
0110 |
0110 |
1000 |
1000 |
1000 |
|
11 |
1100 |
1001 |
1001 |
1001 |
- |
- |
- |
- |
- |
- |
4.Обозначаем символами ![]() внутренние состояния автомата в последующем
такте
внутренние состояния автомата в последующем
такте
![]() и составляем для них «по
единицам» логические уравнения, используя таблицу переходов(в каждой клетке
таблицы левый бит характеризует сигнал
и составляем для них «по
единицам» логические уравнения, используя таблицу переходов(в каждой клетке
таблицы левый бит характеризует сигнал ![]() ,
следующий бит -
,
следующий бит - ![]() , дальше -
, дальше - ![]() , а правый бит -
, а правый бит - ![]() ).
).
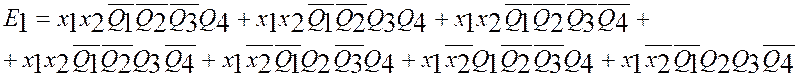
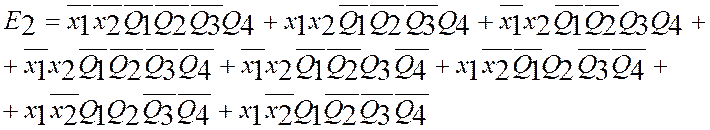 |
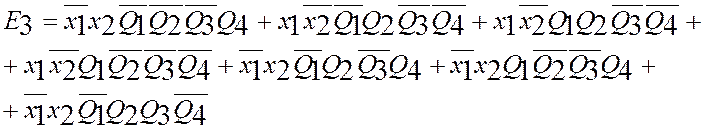
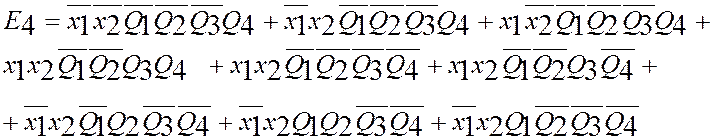 |
Минимизируем полученные ФАЛ, таким образом, чтобы получилось как можно меньше термов в записи ФАЛ.
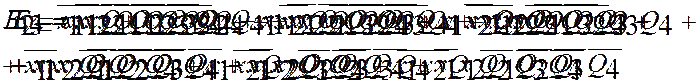 |
5.Принимаем, что входные, выходные сигналы и внутренние состояния будут храниться в регистрах В, С и D соответственно в виде байтов: 0000
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.