Расчет сложной цепи методом контурных токов, страница 2

 ,             ,            

Главный определитель системы  D

            = 8875

Дополнение D₁ получается заменой первого столбца главного определителя столбцом свободных членов

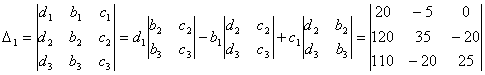=35500

Дополнение D₂ получается заменой второго столбца главного определителя столбцом свободных членов

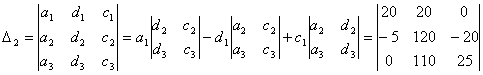= 106500

Дополнение D₃ получается заменой третьего столбца главного определителя столбцом свободных членов

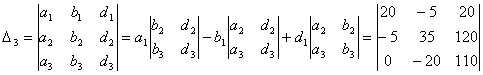  = 124250

Величины контурных токов

 ,             ,         

1-ая и 2-ая ветви. Величина и направление тока 1-ой ветви I₁  и 2-ой ветви I₂ совпадает с контурными токами I₁₁.и I_22. Соответственно I₁= I₁₁ = 4 А, I₂.= I₂₂ = 12А 

3-я ветвь. Величина и направление тока 3-ой ветви I₃ будет складываться из  контурных токов I₁₁ и I₂₂ Следовательно I₃= I₂₂ - I₁₁  = 12-4 = 8А;

4-ая ветвь. Величина и направление тока 4-ой ветви I₁ совпадает с контурным током I₃₃. Следовательно I₄= I₃₃ = 14 А

5-ая ветвь. Величина и направление тока 5-ой ветви I₅ будет складываться из  контурных токов I₂₂ и I₃₃ Следовательно I₅= I₃₃ - I₂₂  = 14-12 = 2А;

Проверка, через баланс мощностей:

120*4+100*8+20*12+110*14=3060

=16*15+144*10+64*5+4*20+196*5=3060

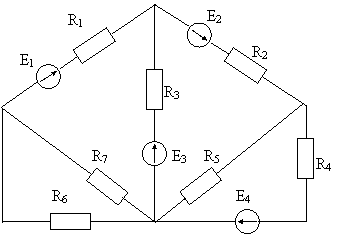
Вариант № 16

Параметры схемы

Источники питания: Е₁ = 120 В,   Е₂ = 20 В,    Е₃ = 100 В, Е₄ =  110 В.

Сопротивления: R₁ = 5 Ом, R₂ = 10 Ом, R₃ = 5 Ом, R₄ = 5 Ом, R₅ = 20 Ом, R₆ = 20 Ом.
 R₇ = 20 Ом

Выберем произвольные направления токов в ветвях.

Величины токов в ветвях схемы определяем методом контурных токов. Направления обхода контуров контурными токами I₁₁,  I₂₂ , I₃₃ показаны на рисунке. Составляем систему контурных уравнений на основании второго закона Кирхгофа.

,

,

,

где       R₁₁ = R₁ + R₃ + R_5,7- собственное сопротивление 1-го контура,

R₂₂ = R₂ + R₃ + R₆ - собственное сопротивление 2-го контура,

R₃₃ = R₆ + R₄ - собственное сопротивление 3-го контура.

R₁₂ = R₂₁ =  - R₃ - взаимное сопротивление между 1-ым  и 2-ым контурами.