Передаточная функция разомкнутой системы K(p). Передаточная функция и дифференциальное уравнение замкнутой системы, страница 2

ω	Re	Im	ω	Re	Im	ω	Re	Im	ω	Re	Im
0	96.00	0	1.1	–71.47	252.4	8	–8241	1333	21	–35810	–4424
0.1	94.61	23.1	1.2	–103.26	275.1	9	–10280	1347	24	–36720	–8299
0.2	90.46	46.1	1.3	-137.80	297.7	10	–12460	1306	27	–32040	–13470
0.3	83.53	69.2	1.4	–175.08	320.2	11	–14770	1205	30	–19630	–20100
0.4	73.83	92.2	1.7	–303.68	387.2	12	–17170	1039	31	–13370	–22660
0.5	61.37	115.2	2.0	–456.17	453.4	13	–19620	800	32	–5896	–25410
0.6	46.13	138.2	3	–1141	665	14	–22080	483	33	2897	–28350
0.7	28.14	161.1	4	–2088	859	15	–24520	83	34	13111	–31490
0.8	7.38	184.0	5	–3287	1028	16	–26880	–408	35	24840	–34840
0.9	–16.15	206.9	6	–4724	1168	18	–31190	–1684	36	38200	–38390
1.0	–42.43	220.7	7	–6382	1271

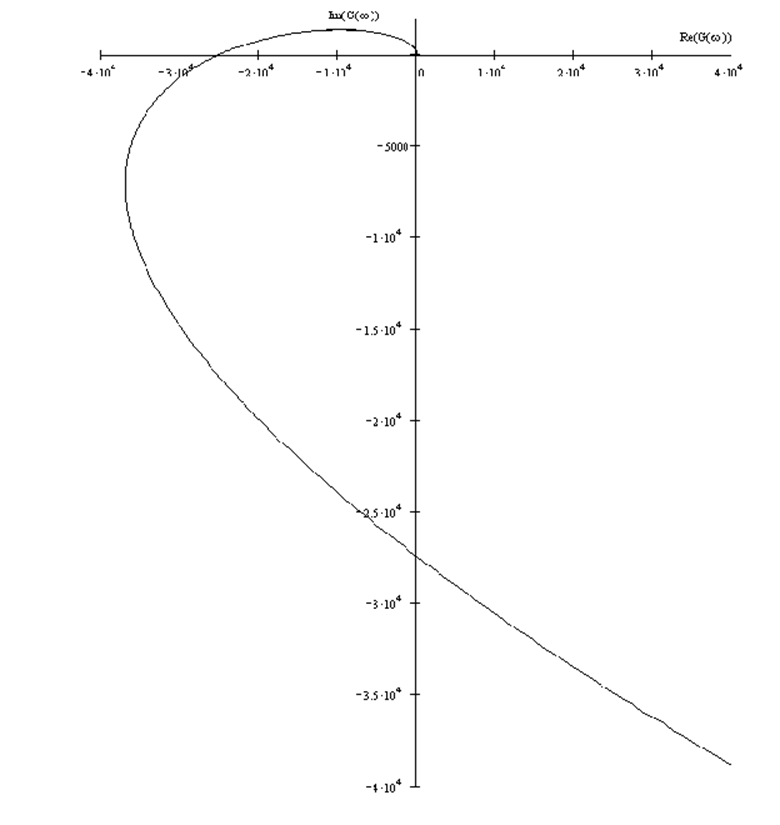8.  Анализ устойчивости с помощью критерия Найквиста. Построение годографа Найквиста.

Коэффициент передачи разомкнутой системы:

ω	Re	Im	ω	Re	Im	ω	Re	Im	ω	Re	Im
0.00	95.0	0.0	3.00	–21.2	–64.7	7.0	–12.9	–11.4	16	–3.64	–2.00
0.25	93.6	–4.8	3.25	–22.1	–55.4	7.5	–11.8	–9.7	18	–2.95	–1.00
0.50	96.2	–5.1	3.50	–22.2	–47.9	8.0	–10.9	–8.4	20	–2.43	–0.73
0.75	108.0	–8.0	3.75	–21.8	–41.9	8.5	–10.0	–7.2	22	–2.04	–0.56
1.00	127.0	–23.0	4.00	–21.2	–36.9	9.0	–9.2	–6.3	24	–1.73	–0.44
1.25	141.7	–60.8	4.25	–20.5	–32.7	9.5	–8.5	–5.5	26	–1.49	–0.35
1.50	123.8	–113.7	4.50	–19.8	–29.2	10	–7.9	–4.8	28	–1.29	–0.28
1.75	72.0	–140.7	4.75	–19.2	–26.2	11	–6.8	–3.8	30	–1.13	–0.23
2.00	25.9	–132.0	5.00	–18.2	–23.6	12	–5.9	–3.0	32	–1.00	–0.19
2.25	–0.1	–111.4	5.50	–16.7	–19.3	13	–5.2	–3.8	34	–0.89	–0.16
2.50	–12.8	–92.1	6.0	–15.3	–16.1	14	–4.6	–3.0	36	–0.79	–0.13
2.75	–18.6	–76.7	6.5	–14.0	–13.5	15	–4.1	–2.4	38	–0.71	–0.11

То есть по критерию Найквиста обозначает что система устойчива.

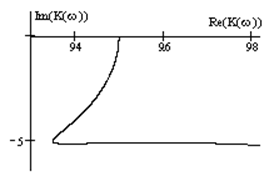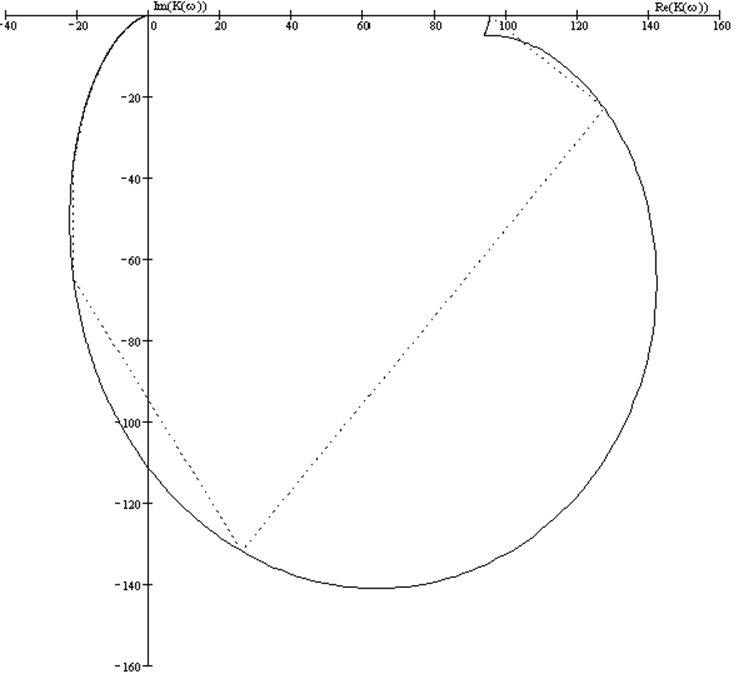
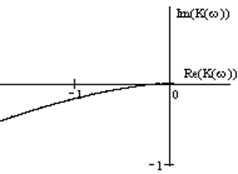
Определение запаса устойчивости по фазе  и по модулю.

По определению запас устойчивости по модулю:

Запас устойчивости по модулю равен расстоянию между критической точкой (-1; 0) и точкой пересечения годографа с вещественной осью, т.е. разницей между единицей и модулем K(f) на той частоте, где связь стала положительной.

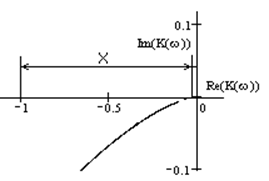
То есть запас устойчивости по модулю составляет практически единица.  X = 1, или в дБ бесконечность.

Определение запаса устойчивости по фазе:

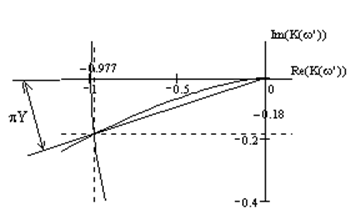
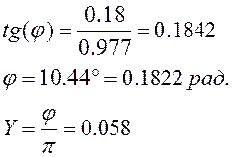
9.  Определение ошибки регулирования  и построения графика.

Передаточная функция для ошибки от регулирующего воздействия

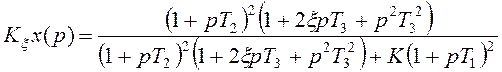
Запишем передаточную функцию для ошибки от регулирующего воздействия следующим образом:

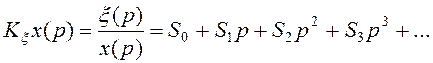
Тогда можно записать,  что

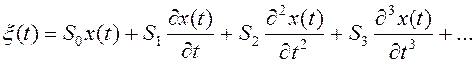
Выразим коэффициенты S_iчерез известные коэффициенты G_i и A_i

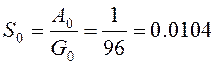
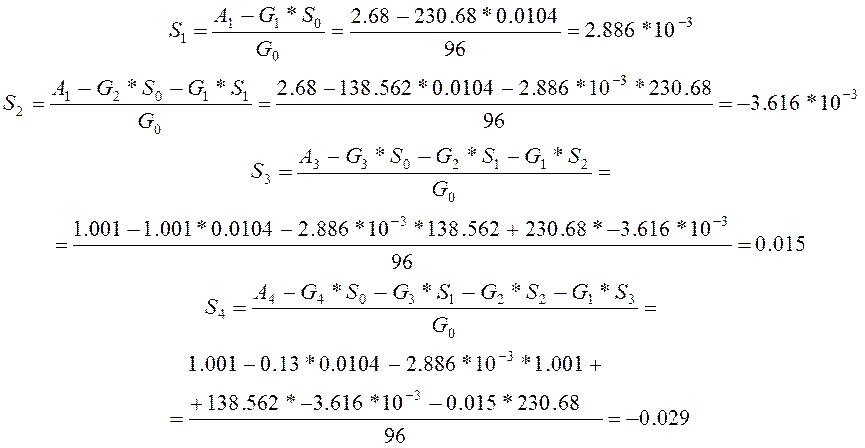
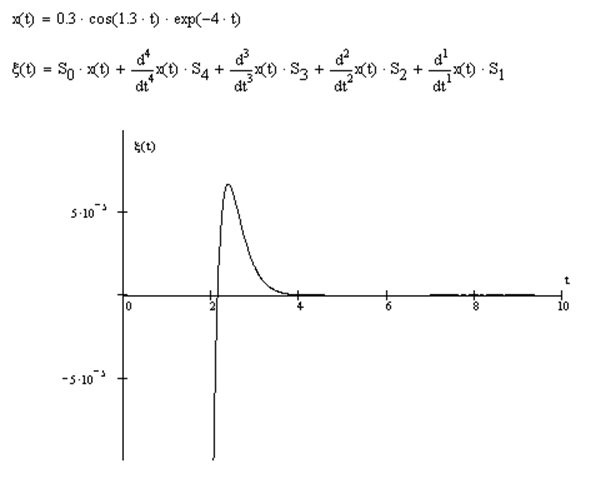
Дополнение к выполненной работе:

Произодные для пункта 9:

Известно, что входной сигнал имел вид:

Тогда соответственно производные будут выглядеть следующим образом:

Первая производная: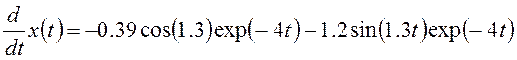

Вторая производная

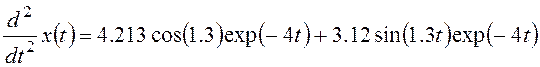
Третья производная

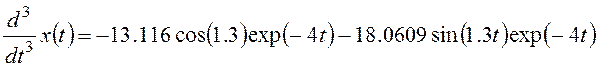
Четвертая производная

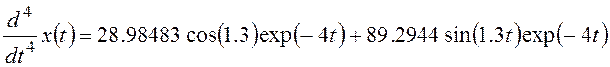
Используемая литература:

1.  Конспект лекций

2.  Радиоавтоматика. Методические указания к самостоятельной аудиторной работе (САР). Новосибирск – 1990.

3.  Радиоавтоматика. Методические указания. Новосибирск – 1995.