Расчет площади поперечных сечений стержней системы, определение величины осевых усилий и напряжений в стержнях системы, страница 2

=1,71∙10⁴ Н

S₂===2,992∙10⁴ Н

Проверка:

1,71∙10⁴∙1∙1+2,992∙10⁴∙0,7∙(1+1,5)=2∙10⁴∙(1+1,5+1)+0∙(1+1,5-0,5)

6,9∙10⁴7∙10⁴

Окончательно: S₁=1,71∙10⁴ H (растяжение); S₂=-2,992∙10⁴ Н (сжатие)

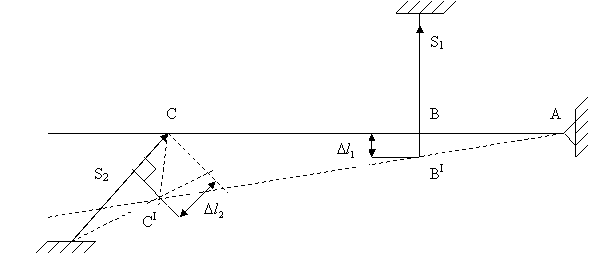
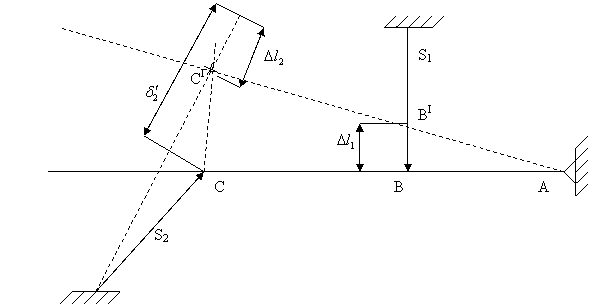
(2)     Определение напряжений, вызванных неточностью изготовления:

δ₂=δ∙l₂   δ₂=   2-й стержень удлинен.   При сборке он сжимается, балка поворачивается по часовой стрелке и 1-й стержень тоже сжимается.

 

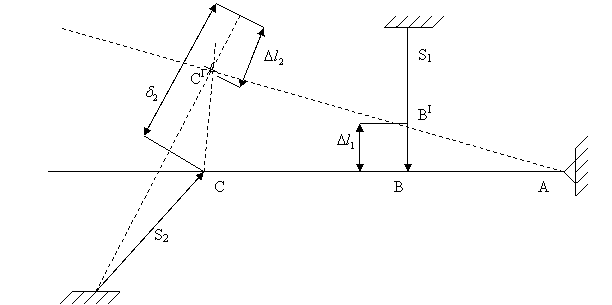
Уравнения статики:

      

Уравнение совместимости деформаций:

===k=

По закону Гука: =   =

Отсюда +k∙=

=

Из уравнений статики получим: =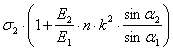

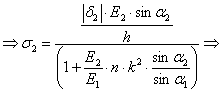σ₂=6,84 МПа  

σ₁=n∙k∙σ₂=2∙1,768∙6,84=24,183 МПа  

Проверка:

24,183=2∙1,768∙6,84

24,183=24,186

Окончательно: σ₁=-24,183 (сжатие); σ₂=-6,84 (сжатие)

(3)                        Расчёт температурных напряжений.

При нагревании 2-й стержень удлиняется    

При сборке он сжимается, балка поворачивается по часовой стрелке и 1-й стержень тоже сжимается.

Уравнения статики:

   S₁-k∙S₂=0   S₁=k∙S₂    

Уравнение совместимости деформаций:

===k=

Уравнения отличаются от уравнений в п.2 только правой частью. Поэтому аналогично как в п.2 получим:

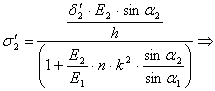
=11,7 МПа

2∙1,768∙11,7=41,371 МПа

Проверка:

41,371=2∙1,768∙11,7