i. Время
действия сигнала
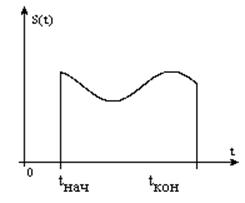 Tc=tкон
– tна
Tc=tкон
– tна
ii. Полоса
частот сигнала
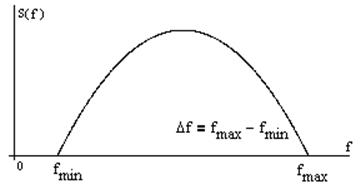
iii. База сигнала Bc=TcDfc Cигналы с малой базой Bc~1 Сигналы с большой базой (цифровые сигналы) Bc>>1
iv. Динамический
диапазон сигнала
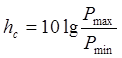
v. Объем
сигнала
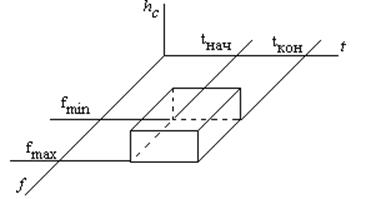 Точно такие же характеристики вводятся и для средств СПИ.
Точно такие же характеристики вводятся и для средств СПИ.
VСПИ > VC Только при соблюдении данного условия возможна передача информации без искажения.
b. Основные энергетические характеристики
i. Мгновенная
мощность сигнала
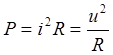 Замечание В теории сигналов сопротивление R
= 1 Ом, то есть
Замечание В теории сигналов сопротивление R
= 1 Ом, то есть
S(t) = i(t) = u(t), То есть можно сказать что энергия сигнала равняется Р = S2(t) (амплитуда)2
ii. Энергия
сигнала на интервале [ti; t2]
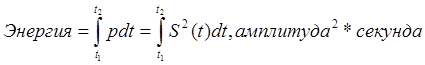
iii. Средняя
мощность сигнала на интервале [ti; t2]
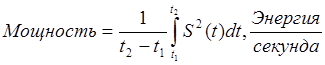
iv. Замечание
Все эти энергетические характеристики не обладают свойством аддитивности
(Например Энергия суммарного сигнала не равна энергии составляющих
сигнала).Разница между ними называется энергией взаимодействия.
S(t)=S1(t)+S2(t),
где соответственно Каждому сигналу соответствует энергия Э1 и Э2,
а S(t) – Э, где Э
¹ Э1 + Э2
Доказательство:
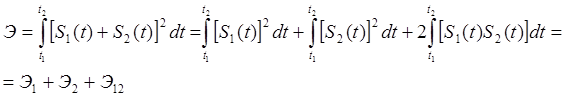 Э12 называется энергией взаимодействия
Если Э12=0 то сигналы называются ортогональными.
Э12 называется энергией взаимодействия
Если Э12=0 то сигналы называются ортогональными.
4. Модели сигналов. Функция включения. Дельта-функция.
Математическая модель сигнала – это аналитическое выражение сигнала , в котором аргументом является время t.
a. Для
того чтобы абстрагироваться от несущественных характеристик сигнала, то есть
для выделение главных характеристик.
Пример
S(t)=Umcos(w0t+j) + n(t) (шум) n(t) ®s(t)
® среднеквадратичное
отклонение. 
Если Um >> s то шумом можно пренебречь.
b. Для обобщения свойств S(t) , т.е абстрагирование самого физического процесса
c. Функция
включения
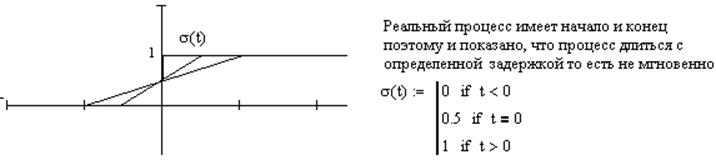
d. Дельта-Функция
или функция Дирака
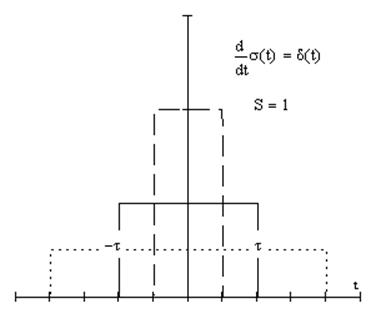
5. Динамическое представление сигналов
a.
С помощью функции Хевисайда
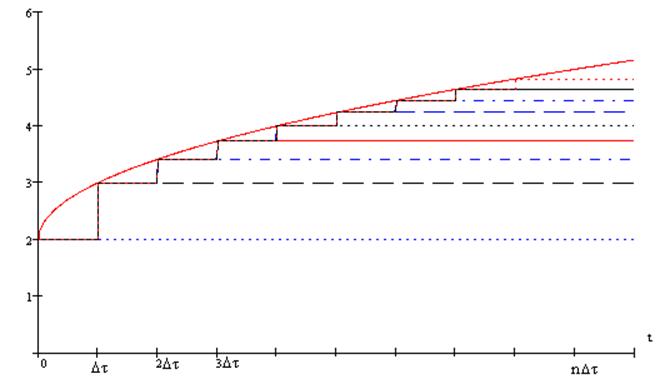
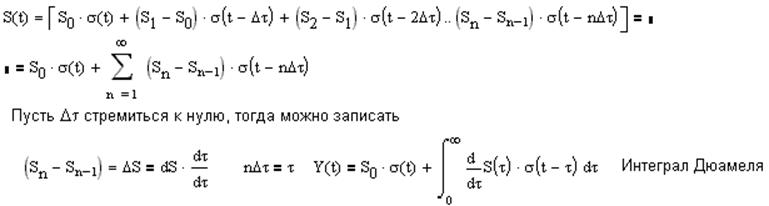
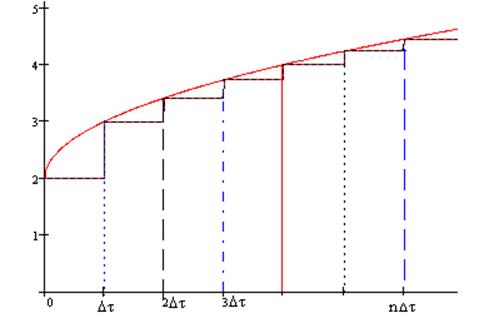
b.
С помощью дельта функции (коротких импульсов)
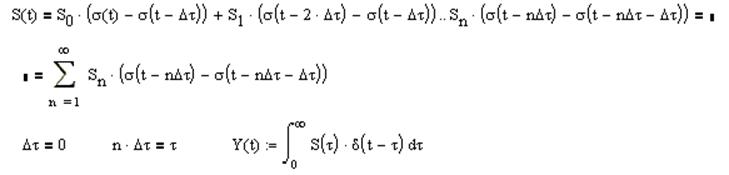
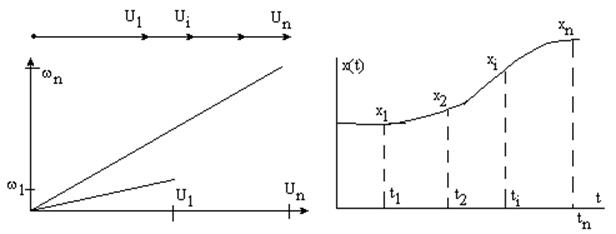
x(t) – (x1, x2, … xi, xn) n – осей и n – проекций и n – мерное пространство
i. Любой сигнал Si(t) - UiÎM является вещественным
ii. UÎM; VÎM; то W = U + V Î M при этом аддитивность a + b = b + a ассоциативность (v + u) + w = v + (u + w)
iii. Если есть сигнал Si(t) ® UiÎM и вещественный коэффициент a, то f=aUi, Î M
iv. В любой системе координат вводится понятие нулевого вектора Æ такой что u + Æ = u
v. Пример нелинейного пространства есть базис из периодических гармонических сигналов.
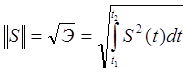 t1 – начало сигнала
t2 – окончания сигнала,
то есть величина ограничения.
Аксиомы
t1 – начало сигнала
t2 – окончания сигнала,
то есть величина ограничения.
Аксиомы
i. ![]()
ii.
iii. SÎM; and a, f =aSÎM
iv. uÎM, vÎM……w= v + u Î M
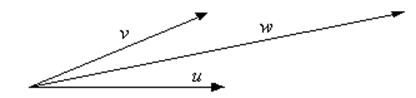
v. Неравенство
треугольника
![]()
vi. Пространство называется нормированным если для него введено операция норма и выполняется вышеприведенные аксиомы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.