Общие сведения о нелинейных цепях и методах их исследования. Аппроксимация характеристик НЭ. Выбор класса аппроксимирующей функции

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО КУРСУ PTЦиC (часть 2)

1.  Общие сведения о нелинейных цепях и методах их исследования.

Общие сведения:

Линейные цепи – цепи, к которым применим принцип суперпозиции, то есть наложения.

   Нелинейные цепи –   цепи, к которым не применим принцип суперпозиции, и они описываются нелинейными уравнениями.

Нелинейные цепи содержат нелинейные элементы, причем они могут быть активными (транзисторы, лампы, интегральные микросхемы) и реактивные (емкости, зависящие от напряжения C(u) – варакторы, варикапы, индуктивности, зависящие от тока (L(i)))

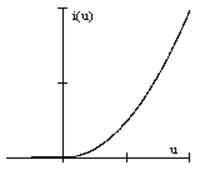i(u) – нелинейная функция, допустим Вольт – амперная характеристика диода.

Не выполнение принципа суперпозиции для  ВАХ, будет означать следующее, что если выполняется следующее условие u₁ + u₂ = u(t), то не обязательно, что выполняется условие i(u₁) + i(u₂) = i(u), скорее наоборот.

Пусть i = au², тогда i = a(u₁ + u₂)² = au₁² + au₂² + 2au₂ u₁ = i₁ + i₂ + 2au₂ u₁. Где последнее слагаемое результат взаимодействия.

Итак из вше сказанного, можно сразу сказать, что принцип суперпозиции не применим.

Линейная цепь - > на выходе по сравнению со входом не дает новой функции. (либо столько, либо меньше).

Нелинейная цепь -> дает новые функции на выходе (трансформация спектра).

Рассмотрим ВАХ диода.

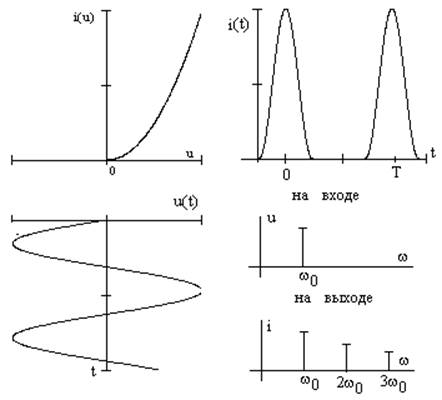Периодическое, но негармоническое колебание, разлагается в ряд Фурье в n-число гармоник, до бесконечности.

Для исследования линейных цепей есть методы:

Спектральный метод

Интеграл Дюамеля

Классические

Для исследования линейных цепей можно   представить три групп:

1. Графические методы исследования, из примера, который был приведен выше можно заключить, что в данном методе можно качественно оценить, что будет на выходе.

2. Аналитические методы исследования

3. Графо-аналитические методы исследования.

Исследования преобразований сигналов в нелинейных цепях:

Анализ (цепи, сигнала) и синтез (цепи, сигнала)

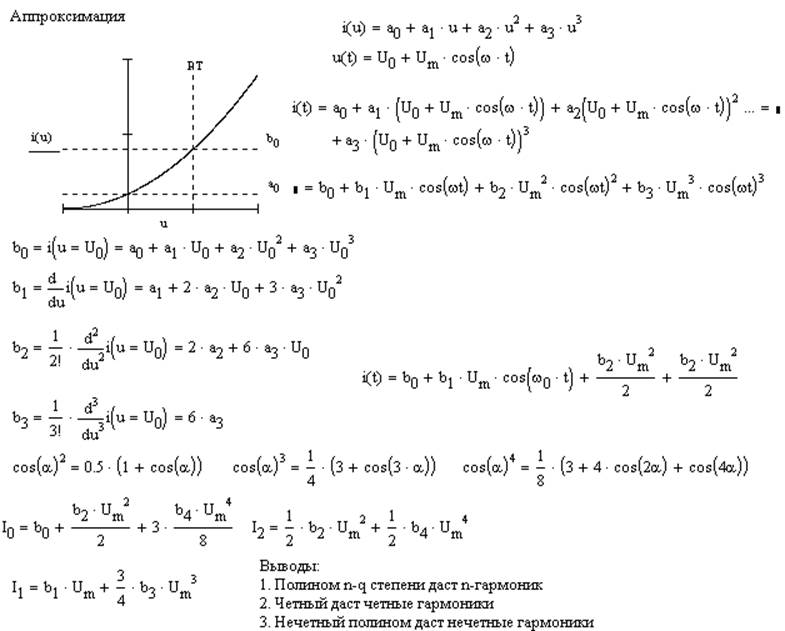
2.  Аппроксимация характеристик НЭ. Выбор класса аппроксимирующей функции.

Аппроксимация -  это аналитическое описание, графически, таблично или аналитически заданных характеристик цепи с помощью подходящих функций.

Задача аппроксимации:

-  Выбор подходящей аналитической функции

- Определение ее коэффициентов

Часть 1. Выбор подходящей аналитической функции

От чего зависят (чем определяется)

a)  От вида характеристики Нелинейного элемента

b)  От поставленной задачи преобразования сигнала

c)  От ясности физического понимания процесса в цепях

d)  От параметров входного сигнала

Требования к функции

a)  Простота

b)  Точность

c)  Ясность физического понимания

В рабочей точке подходит следующие функции:

a)  Степенной полином

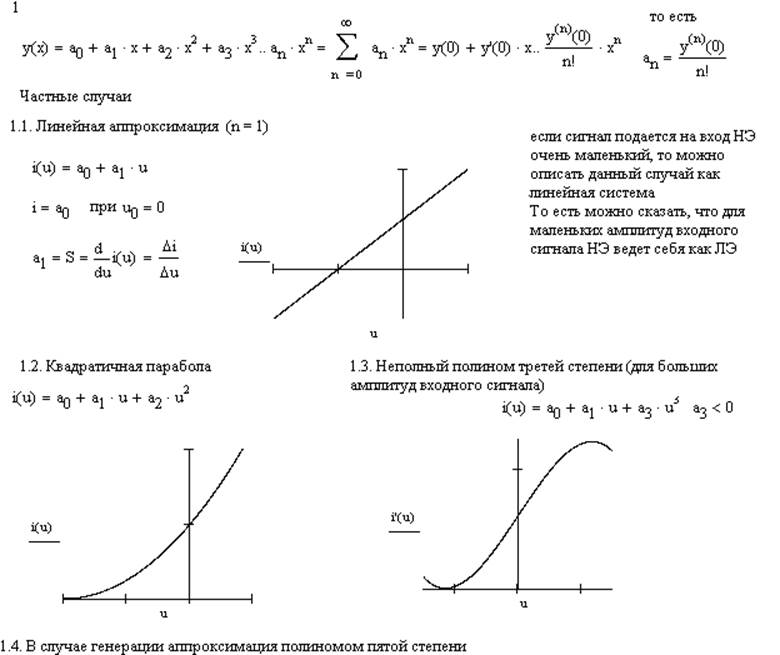
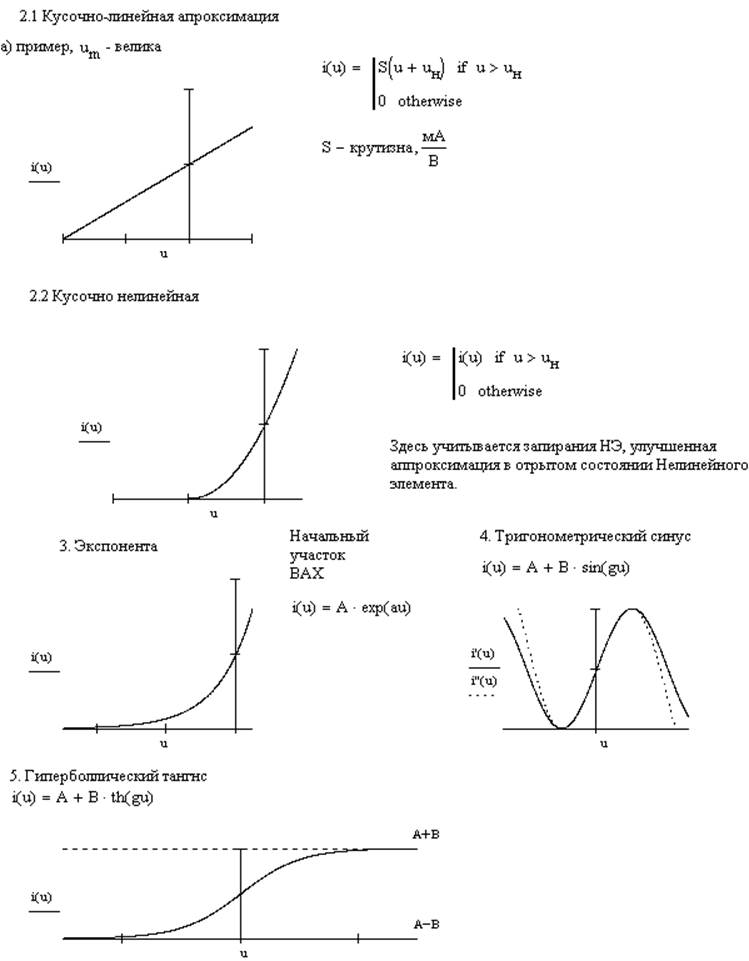
3.  Определение коэффициентов аппроксимирующей функции.

4. 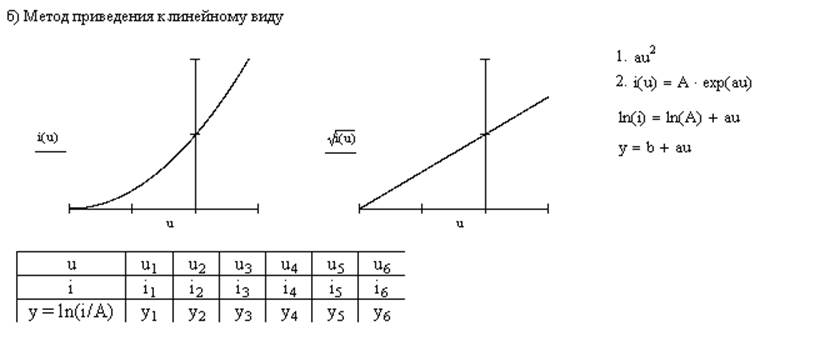 Метод спектрального анализа НЦ с использованием формул 3-х и  более ординат.

4.1  Классический метод спектрального анализа

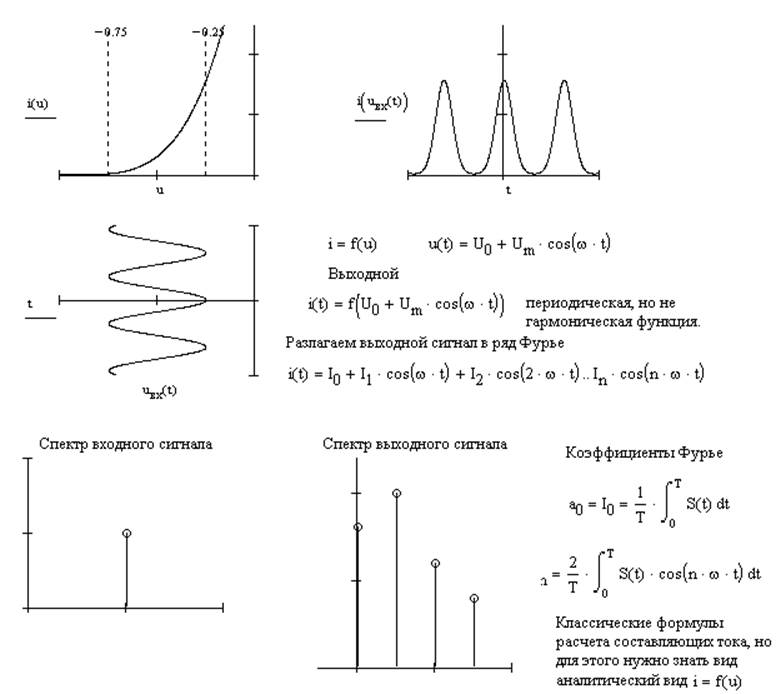
4.2  Формула трех ординат

(Этот  метод применим и для аппроксимированной функции, так и при ее отсутствии).

4.3 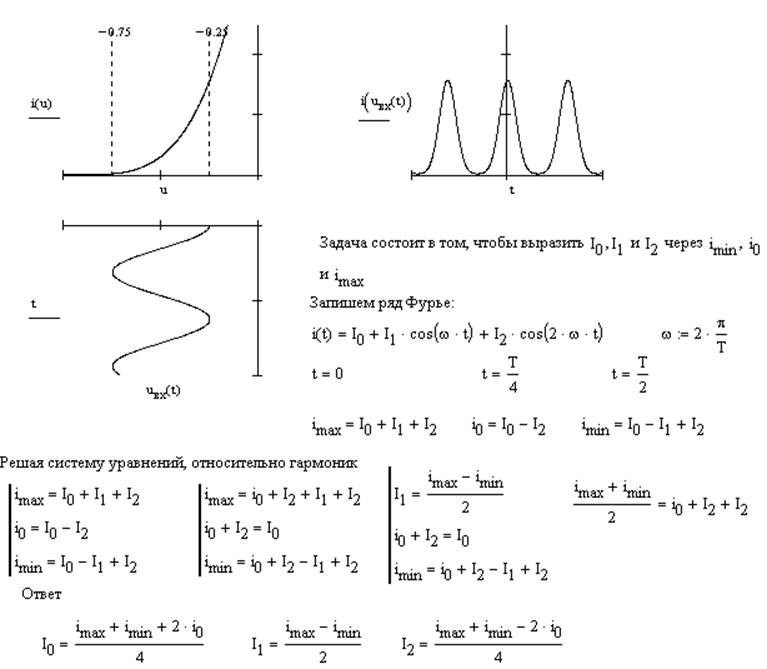 Метод пяти ординат

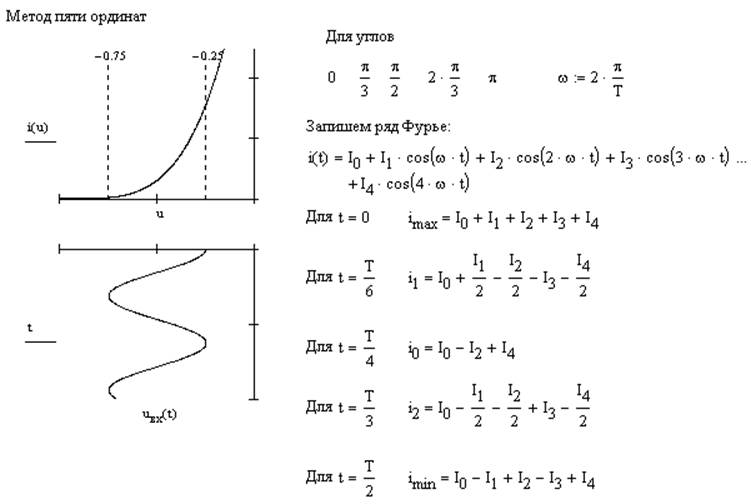
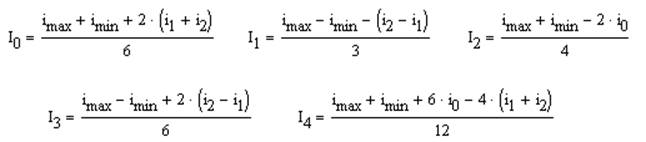
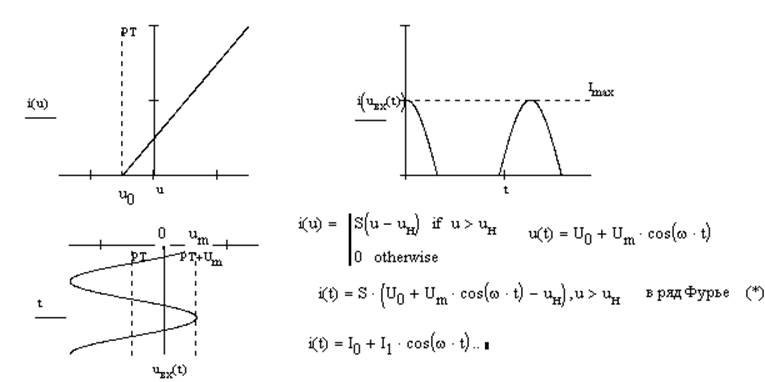
5.  Метод спектрального анализа НЦ с использованием формул кратных дуг.

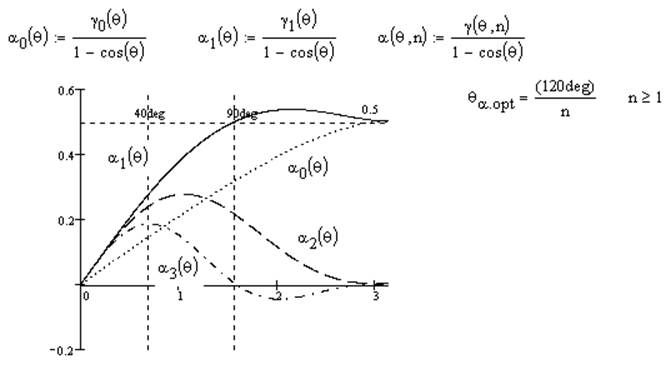
6.  Метод спектрального анализа НЦ с использованием угла отсечки и функций Берга.

7.  Метод спектрального анализа НЦ с использованием модифицированных функций Бесселя.

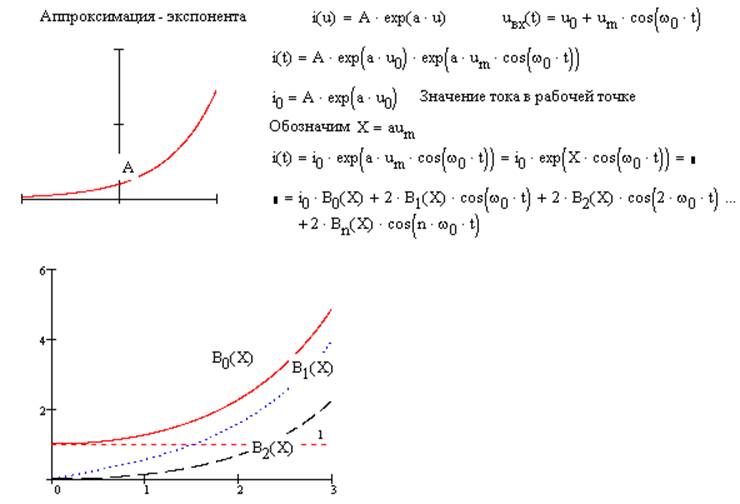
8.  Метод спектрального анализа НЦ с использованием обычных функций Бесселя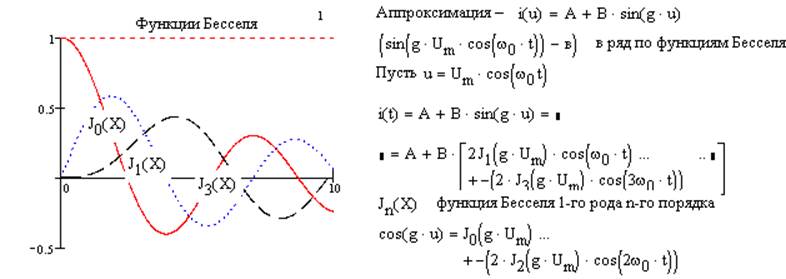

9.  Случай бигармонического сигнала. Теория комбинационных частот.

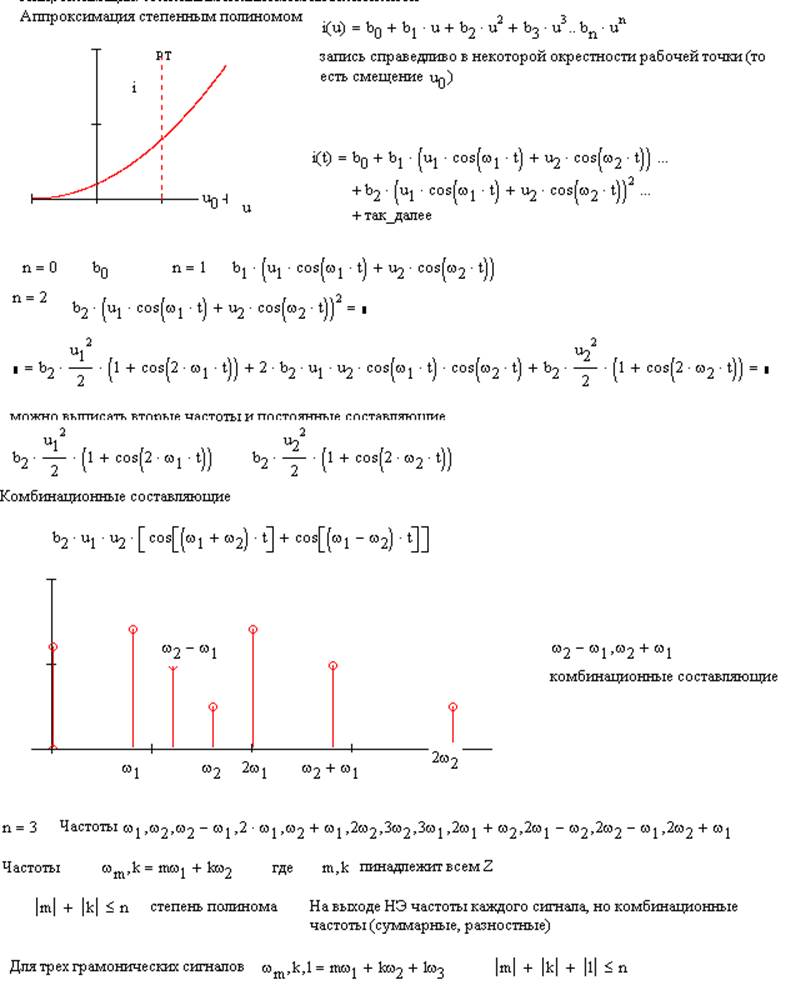
10.  Прохождение случайных процессов (СП) через НЦ. Одномерные законы распределения вероятностей СП на выходе безынерционных НЦ. Пример.

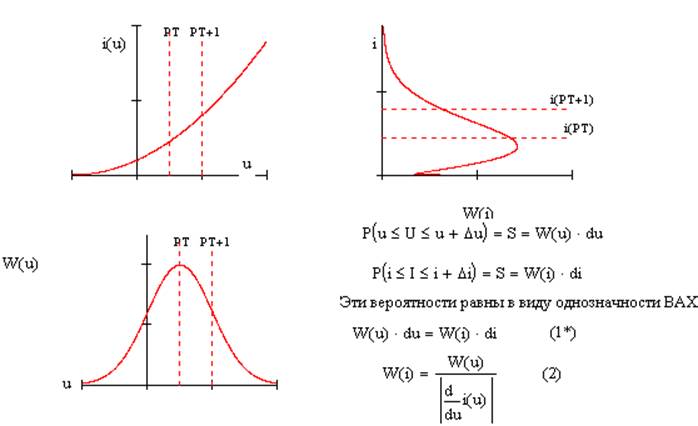Пример: