Расчет оптимального плана и максимальной прибыли производства, страница 2

Получаем план . Так как все коэффициенты  при свободных переменных (x₃ и x₄) неотрицательны, то получаем план , который является оптимальным; так как при свободных переменных (x₃ и x₄) нет коэффициентов , равных нулю, план единственный, а значение целевой функции при нем равно:

Проверка:  (верно)

Ответ: оптимальный план производства , а максимальная прибыль при нем равна 77 рублей 20 копеек.

Задание 2

 

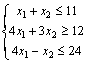
Сначала приведем задачу к каноническому виду: для этого задачу максимизации сделаем задачей минимизации , а в неравенства ограничений добавим балансовые переменные таким образом, чтобы неравенства превратить в равенства.

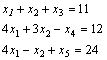
После этого добавляем искусственные переменные: так как в исходной (нерасширенной) матрице есть два правильных столбца, а ранг исходной матрицы равен трем, то необходимо добавить только одну искусственную переменную x₆, т.е.

              

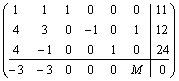
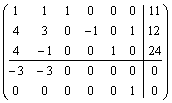
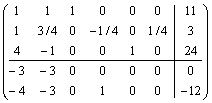
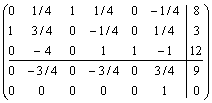
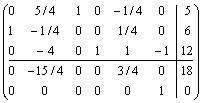
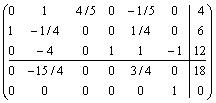
Так как искусственная переменная (x₆) равна нулю и все коэффициенты  при свободных переменных (x₃ и x₅) неотрицательны, то существует оптимальный план. Так как при свободной переменной x₅ , то существует бесконечное множество решений (альтернативных оптимальных планов), которые можно описать следующим образом:

Пусть , тогда выпишем остальные переменные выражая их через x₅.

  

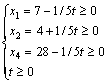
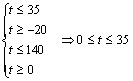
Таким образом, получаем следующий план: . Тогда оптимальный план будет следующим:  при , т.е.

Максимальное значение целевой функции равно при этом 33.

Проверка: .

Задание 3

Исходные данные:

- матрица стоимости перевозок единицы товара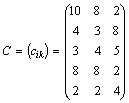

- величины