Фазоманипулированные сигналы в системах связи, страница 2

i	fi-1	fi-2	fi-3	fi-4	fi
0	1	1	0	1	1
1	1	1	1	0	0
2	0	1	1	1	1
3	1	0	1	1	1
4	1	1	0	1	1
5	1	1	1	0	0
6	0	1	1	1	1
7	1	0	1	1	1
8	1	1	0	1	1
9	1	1	1	0	0
10	0	1	1	1	1
11	1	0	1	1	1
12	1	1	0	1	1
13	1	1	1	0	0
14	0	1	1	1	1
15	1	0	1	1	1

Вывод:   от изменения коэффициентов b_k зависит период последовательности.

4.2.  Корреляционные функции М-последовательностей.

Рассчитаем АКФ одиночной М-последовательности с коэффициентами 1001

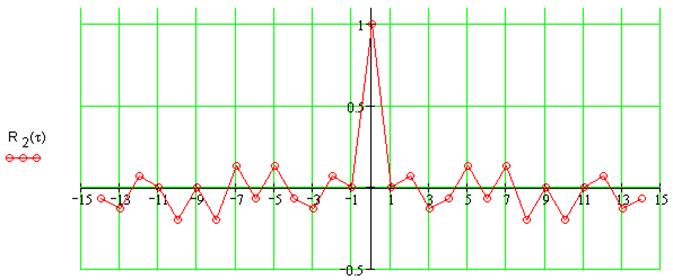
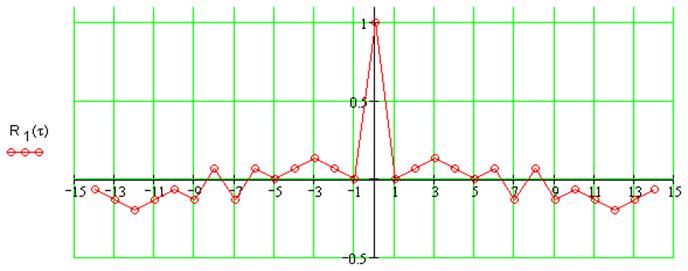
Рассчитаем АКФ периодической последовательности с коэффициентами 1001

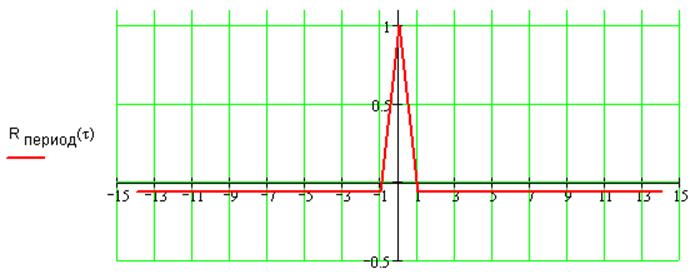
Рассчитаем АКФ одиночной М-последовательности с коэффициентами 0001

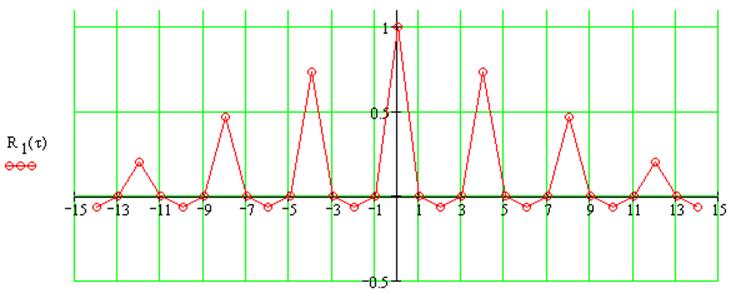
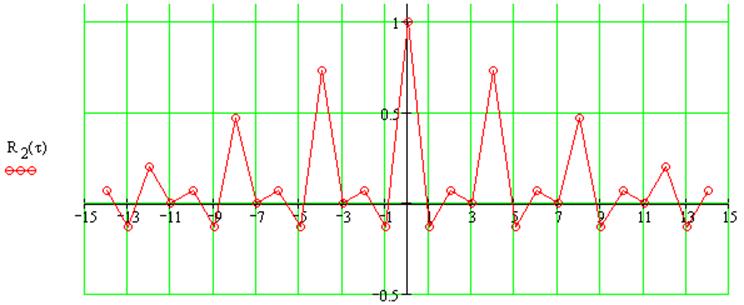
Рассчитаем АКФ периодической последовательности с коэффициентами 0001

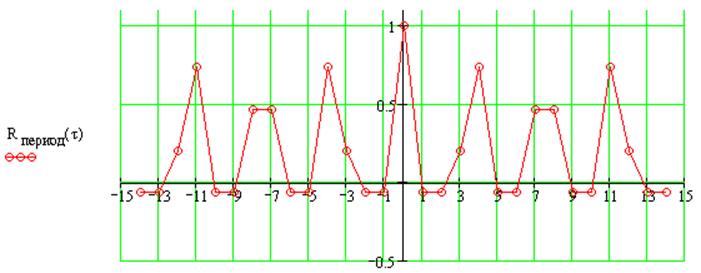
Рассчитаем ВКФ одиночных последовательностей:

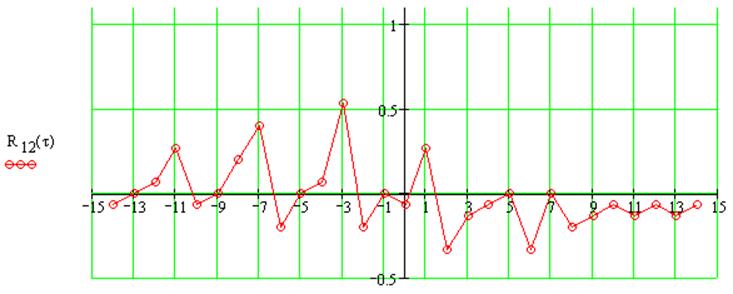
Рассчитаем ВКФ периодических последовательностей:

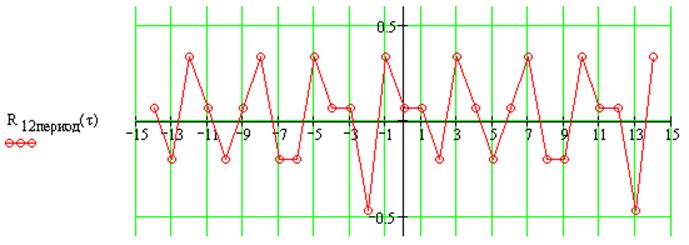
Вывод: при сдвигах  непериодических последовательностей АКФ и ВКФ равны нулю. АКФ одиночных М-последовательностей и периодических – различны. При равной длине периодических последовательностей, их АКФ одинаковы.

4.3.  Генерирование кодов Голда.

3.1.    Рассчитаем ВКФ для периодических М-последовательностей П1 и П2.

Последовательность П1                                          Последовательность П2

Начальная установка регистра - P1=1                   Начальная установка регистра – P2=5

011                                                                        101

i	fi-1	fi-2	fi-3	fi
0	1	0	0	0
1	0	1	0	1
2	1	0	1	1
3	1	1	0	1
4	1	1	1	0
5	0	1	1	0
6	0	0	1	1
7	1	0	0	0

i	fi-1	fi-2	fi-3	fi
0	1	0	1	0
1	0	1	0	0
2	0	0	1	1
3	1	0	0	1
4	1	1	0	1
5	1	1	1	0
6	0	1	1	1
7	1	0	1	0

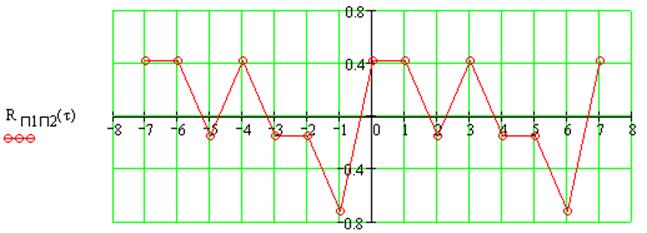
Рассчитаем теоретические значения ВКФ:

                           

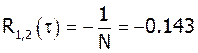
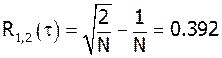
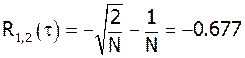
Теоретические значения ВКФ похожи на значения на графике. Из графика видно что ВКФ имеет трехуровневую структуру.

Вывод:  данные М-последовательности применимы для формирования кодов Голда.

4.3.2. Рассчитаем две комбинации кода Голда на основе исходных М-последовательностей

Последовательность П1                                          Последовательность П2

i	fi-1	fi-2	fi-3	fi
0	1	0	0	1
1	1	1	0	1
2	1	1	1	0
3	0	1	1	1
4	1	0	1	0
5	0	1	0	0
6	0	0	1	1
7	1	0	0	1

011                                                                              101

i	fi-1	fi-2	fi-3	fi
0	1	0	0	0
1	0	1	0	1
2	1	0	1	1
3	1	1	0	1
4	1	1	1	0
5	0	1	1	0
6	0	0	1	1
7	1	0	0	0

Коды Голда соответствующие взаимным сдвигам, равным 1 и 2:

i	fП1,i	fП2,(i+1)	fП2,(i+2)	fГ1,i	fГ2,i
0	0	1	0	1	0
1	1	0	1	1	0
2	1	1	0	0	1
3	1	0	0	1	1
4	0	0	1	0	1
5	0	1	1	1	1
6	1	1	1	0	0
7	0	1	1	1	1

4.4.  Корреляционные функции кодов Голда.

ВКФ:

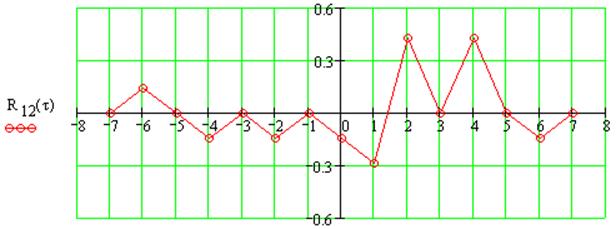
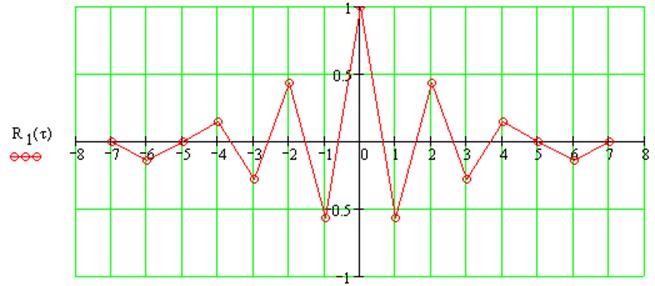
АКФ: