МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра РП и РПУ
Основы компьютерного проектирования и моделирования РЭС.
Расчётно-графическое задание № 1
Вариант № 9
Выполнила:
Студентка: Мироненко Л.
Группа: РТ5-01
Преподаватель: Шлыкова О.Н.
Новосибирск 2012
Задание на работу:
1. Получить амплитудно-частотную характеристику (АЧХ) коэффициента передачи по напряжению заданной схемы при номинальных значениях параметров компонентов. Провести анализ с учетом наихудшего отклонения параметров компонентов от номиналов (режим главного меню “Наихудший случай”).
2. Рассчитать коэффициенты влияния (режим главного меню “Коэффициенты влияния”).
3. Принять решение о способе подстройки схемы с компонентами, имеющими отклонения от номиналов, с целью максимального восстановления исходной характеристики (АЧХ); должны быть апробированы, по крайней мере, два варианта. Смоделировать на ЭВМ процедуру подстройки схемы с целью достижения наилучшего результата (режим главного меню “Регулирование компонентов”).
4. Смоделировать настройку с использованием программы оптимизации (режим главного меню “Оптимизация симплекс-методом”).
5. Сравнить результаты настройки схемы различными парами компонентов; сопоставить результаты настройки схемы на основе использования последовательного интуитивного подбора значений компонентов и на основе использования программы оптимизации; привести аргументы в пользу выбранного вами способа подстройки схемы.
6. Оформить пояснительную записку, описывающую процедуру выполнения задания с выделением этапов принятия решений и их мотивировкой.
Фильтр высоких частот Кауэра
Файл данных RLC.DAT
500., 22000.
R,1000.,0,1,-6.9,10.2
R,1000.,0,4,-9.5,11.4
L,1.533E-2,1,2,-7.2,8.1
L,2.279E-3,2,3,-6.3,9.4
L,2.279E-2,2,4,-9.4,5.7
C,2.153E-8,0,3,-6.9,7.0
C,1.657E-8,0,4,-6.0,6.4
В первой строке записываются значения верхней и нижней частоты рабочего диапазона в герцах. Далее компоненты, значения компонент, номера узлов к которым подключен компонент, положительный и отрицательный процент отклонения данного компонента от номинала.
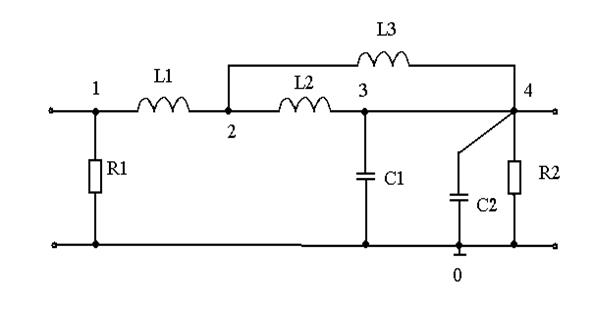
Рис. 1. Схема электрическая принципиальная ФВЧ Кауэра.
1. Снятие АЧХ коэффициента передачи по напряжению заданной схемы.
Задав параметры схемы в файл данных под именем RLC.DAT, запускаем программу NASTR.EXE, в появившемся меню выбираем пункт “худший случай”. Под “худшим случаем” понимается такое отклонение параметров компонентов от номинальных значений, при которых АЧХ максимально отклоняется от идеальной, полученной при номинальных значениях параметров (рис. 2).
Номиналы и отклонения параметров компонентов при наихудшем случае отражены в таблице 1.
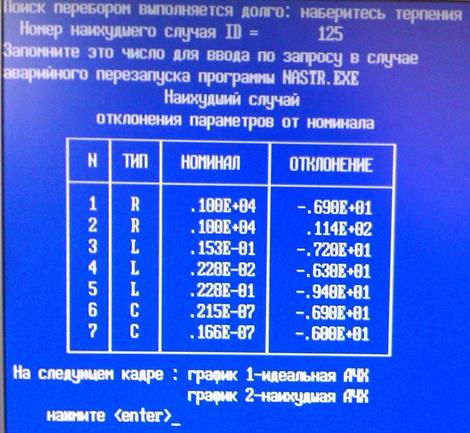
Таблица 1.
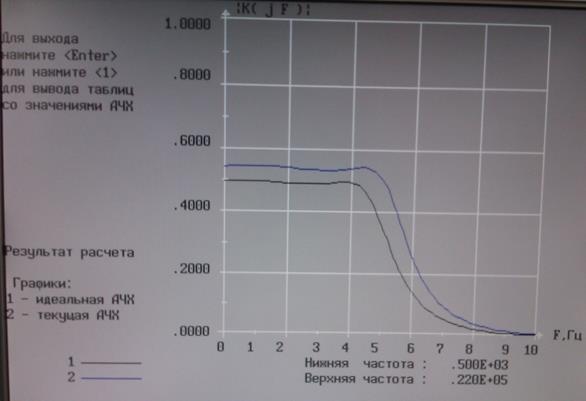
Рис. 2 Идеальная и наихудшая АЧХ схемы ФВЧ Кауэра.
2. Расчет коэффициентов влияния.
Выбираем режим «Коэффициент влияния». Программа рассчитывает относительные коэффициенты чувствительности отклонений номиналов компонентов схемы для одиннадцати равноотстоящих друг от друга частот в пределах заданного интервала, а так же интегральный критерий влияния (SKVL) каждой компоненты на модули коэффициенты передачи на всех одиннадцати частотах.
Результаты расчета приведены в таблице 2.
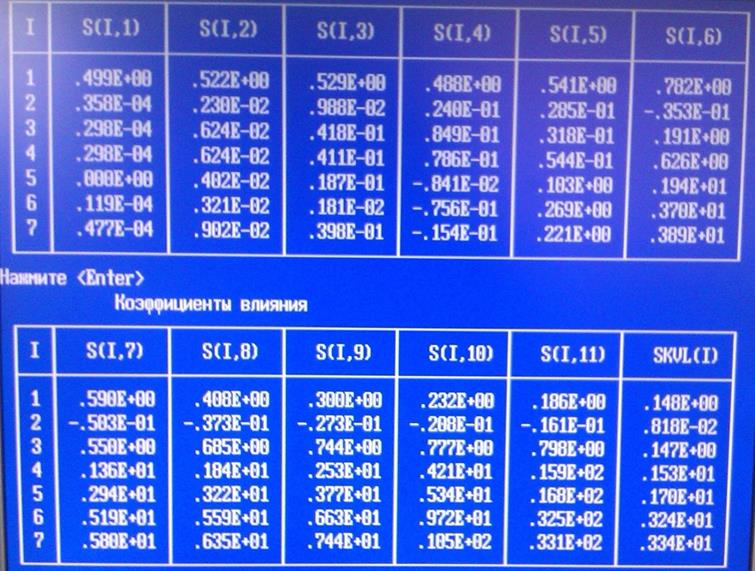
Таблица 2.
Из таблицы 2 видно, что наибольшие коэффициенты влияния имеют элементы 6 и 7 соответственно обозначенные на схеме (Рис. 1) как конденсаторы С1, С2, к тому же, использовать конденсаторы в качестве подстроечных элементов удобно на практике.
3. Ручная подстройка.
Целью подстройки схемы с компонентами, имеющими отклонения от номиналов, является максимальное восстановление исходной характеристики АЧХ. В качестве подстроечных элементов выбираем 6-ой и 7-ой. Запускаем подпрограмму «Регулирование компонент».
1) Выберем элемент, номинал которого будет изменяться в процессе подстройки.
2) Зададимся диапазоном регулирования номинала этого элемента, в процентах, в положительную и отрицательную область.
3) Параметры всех остальных элементов примут значения, соответствующие худшему случаю.
4) Выведем графики идеальной АЧХ и подстроенной АЧХ.
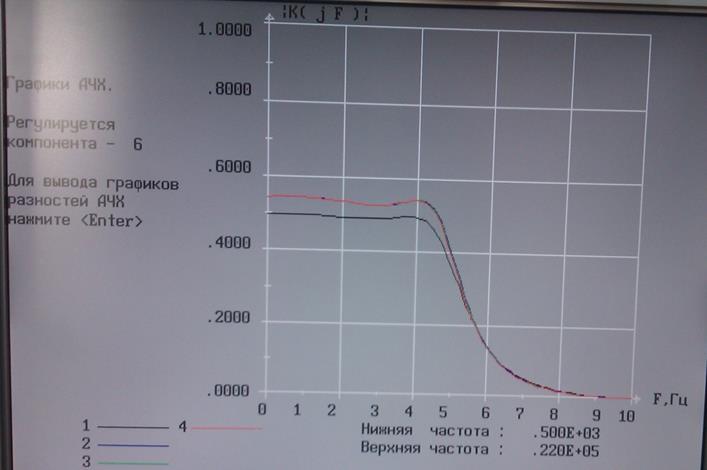
Рис. 3 Идеальная и подстроенная 6–ой и 7-ой компонентой АЧХ.
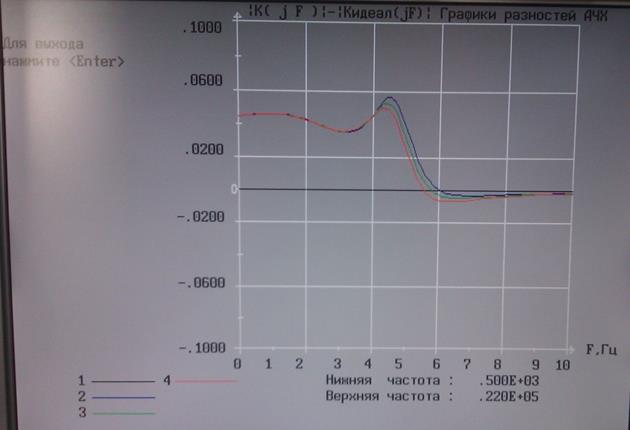
Рис. 4 Разность идеальной и подстроенной 6–ой и 7-ой компонентой АЧХ.
Из графика подстройки двумя компонентами видно, что подстройка реальной АЧХ к идеальной АЧХ 7-ой и 6-ой компонентами не дала хорошего результата. Из этих двух компонент в качестве подстроиечной выберем 6-ую компоненту т.к. она лучше подстраивает реальную АЧХ к идеальной АЧХ. Т.к. подстройка осуществляется парой компонент, просмотрев все компоненты, наиболее подстраиваемой реальную АЧХ к идеальной АЧХ является 2-ая компонента.
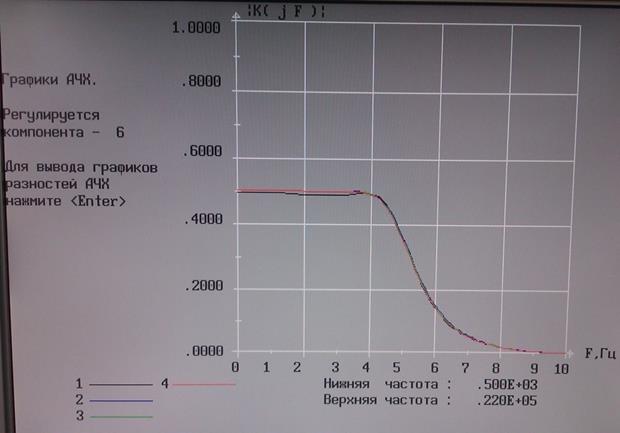
Рис. 5 Результат ручной подстройки 6-ой и 2-ой компонентой АЧХ.
Из графика (рис. 5) видно, что ручная подстройка 6-ой и 2-ой компонентами дала хороший результат.
4. Подстройка симплекс-методом.
Программа SIMPLEX предназначена для поиска значений двух варьируемых компонентов, при которых АЧХ схемы, искаженная за счет разброса параметров компонентов, будет максимально приближена к идеальной.
В главном меню выберем пункт “Оптимизация симплекс-методом”, введем два номера компонента, которыми будет варьировать оптимизирующая программа.(№6 и №7).
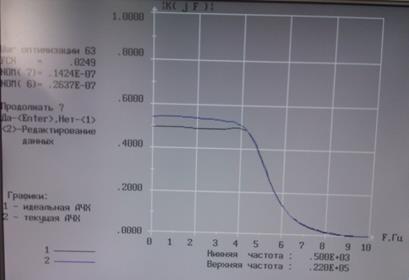
Рис. 6. Результат подстройки 7-ой и 6-ой компонентой симплекс методом.
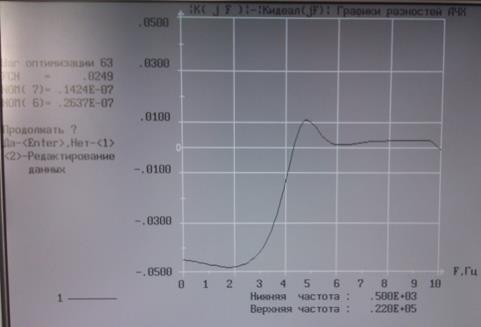
Рис. 7. Разность подстройки 7-ой и 6-ой компонентой симплекс методом.
Введем два номера компонента, которыми будет варьировать оптимизирующая программа.(№6 и №2).
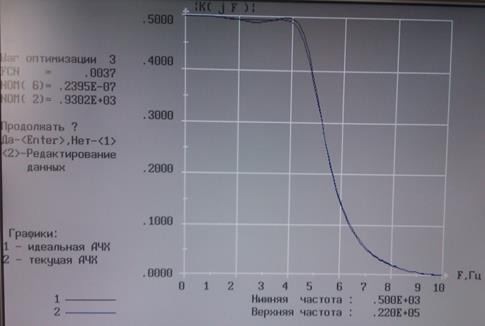
Рис. 7. Результат подстройки 2-ой и 6-ой компонентой симплекс методом.
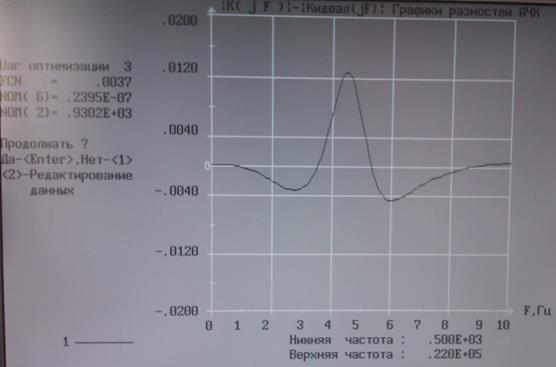
Рис. 8. Разность подстройки 2-ой и 6-ой компонентой симплекс методом.
Симплекс сошелся на 3 шаге.
5. Выводы.
В процессе ручной настройки вызывает затруднение интуитивный подбор отклонений номиналов от наихудшего случая, одновременный учет влияния на АЧХ двух компонент и многократное повторение идентичных операций. Симплекс метод использует алгоритм для двух варьируемых компонентов, что позволяет максимально приблизить искаженную АЧХ к идеальной. Результаты, полученные с помощью обоих методов больших отличий не имеют. Симплекс-метод более удобен, т.к. избавляет пользователя от уже упомянутых повторений идентичных операций.
Достоинство симплекс метода: освобождение от громоздких вычислений, решение полученное симплекс методом максимально приближает искаженную АЧХ к идеальной АЧХ.
Недостатки: Если целевая функция перестала уменьшаться, то функция попала локальный минимум, а значит симплекс метод не сходится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.