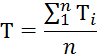
Другие предметы \ Метрология и радиоизмерения

Определение статистических характеристик погрешностей измерений, страница 2

i

, мс

1

20.2257

0.00397

0.00002

2

20.2248

0.00307

0.0001

3

20.2188

-0.00293

0.0001

4

20.2257

0.00397

0.00002

5

20.227

0.00527

0.00003

6

20.2271

0.00537

0.00003

7

20.2173

-0.00443

0.00002

8

20.219

-0.00273

0.00001

9

20.2162

-0.00573

0.00003

10

20.2179

-0.00383

0.00001

11

20.2161

-0.00563

0.00003

12

20.2252

0.00347

0.00001

13

20.2208

-0.00093

0

14

20.2276

0.00587

0.00003

15

20.2167

-0.00503

0.00003

 0.0029

Допустимое значение величины  (из таблицы)

По данным таблицы проводим оценку среднеквадратичного отклонения результатов наблюдений:

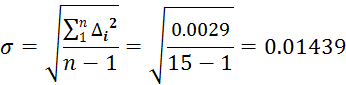
Так же по данным таблицы рассчитаем величину: .

Рассчитаем оценку среднего квадратичного отклонения результата измерения:

И определим интервал погрешности измерения заданной доверительной вероятностью P:

=

Результат измерения представим в виде:

Т=20.22173 мс

P = 0.95

2.2. Обработка результатов наблюдений при заранее неизвестном законе распределения случайных отклонений:

-0.006454

-0.006254

-0.006054

№

Тi

1

20.224

-0.001354

2

20.225

-0.000354

3

20.218

-0.007354

4

20.219

-0.006354

5

20.2188

-0.006554

6

20.2301

0.004647

7

20.2289

0.003546

8

20.2207

-0.004654

9

20.2252

-0.000154

10

20.2302

0.004846

11

20.2301

0.004647

12

20.2303

0.004946

13

20.2301

0.004647

14

20.2277

0.002346

15

20.2264

0.001046

16

20.2187

-0.006654

17

20.2241

-0.001254

18

20.2293

0.003946

19

20.2297

0.004346

20

20.2242

-0.001154

21

20.2248

-0.000554

22

20.2284

0.003046

23

20.2269

0.001546

24

20.221

-0.004354

25

20.2267

0.001346

26

20.2291

0.003746

27

20.2275

0.002146

28

20.2191

-0.006254

29

20.2231

-0.002254

30

20.2197

-0.006254

31

20.2305

0.005146

32

20.2204

-0.004954

33

20.2284

0.003046

34

20.2191

-0.006254

35

20.2216

-0.003754

36

20.2294

0.004046

37

20.2213

-0.004054

38

20.2206

-0.004754

39

20.2298

0.004446

40

20.2299

0.004546

41

20.2193

-0.006054

42

20.2271

0.001746

43

20.2223

-0.003054

44

20.2301

0.004647

45

20.2305

0.005146

46

20.2298

0.004446

47

20.2223

-0.003054

48

20.2291

-0.006254

49

20.2305

0.005146

50

20.2189

-0.006454

   

1011.2677

 =  мс

max = 0.007354

max = - 0.007354

Наиболее близко соответствует гистограмме антимодальная 1 функция.  а= 1.4

σ =  =

σт =

Результат измерения:

Т = 20.225354 мс

σт =

ϕт(∆) – антимодальная 1 функция.

Вывод: На лабораторной работе освоили приемы повышения точности измерений за счет многократных наблюдений измеряемой величины, приобрели навыки работы с цифровым частотомером.

Скачать файл