Предполагая нормальный закон распределения Δ’i проверить fi на наличие грубых погрешностей (промахов). Промахами следует считать наблюдения с отклонением Δ’i, вероятность появления которых меньше выбранного уровня значимости q (рекомендуется выбрать q = 0.05 – 0.01).
По
таблице наибольшего приведенного отклонения находим значение 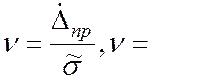 и вычислить
и вычислить ![]() , то
есть отклонения, вероятность появления которых равняется q. Наблюдения которые
больше дельта промаха, считать промахом, так как вероятность их появления
меньше q. Промахи исключить из результатов и рассчитать новые значения
, то
есть отклонения, вероятность появления которых равняется q. Наблюдения которые
больше дельта промаха, считать промахом, так как вероятность их появления
меньше q. Промахи исключить из результатов и рассчитать новые значения ![]() .
.
Определить:
1.
Гистерезис (вариация) показаний ![]()
2.
Систематическую погрешность 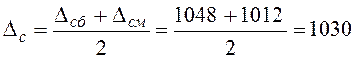
3.
Оценку среднеквадратичного
случайного отклонения результата наблюдений 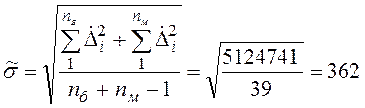
4.
Граничные значения ![]() с доверительной вероятностью Р = 0.95;
с доверительной вероятностью Р = 0.95; ![]() где t(n, P) – коэффициент Стьюдента
(находится по соответствующей таблице через Р и n = nБ + nМ).
где t(n, P) – коэффициент Стьюдента
(находится по соответствующей таблице через Р и n = nБ + nМ).
![]()
Так
как количество измерений сорок, то коэффициент Стьюдента равняется t(n, P) =
2.0. Тогда граничное значение равняется интервала доверительной вероятности ![]()
5. Результату проверки:
|
Тип и номер генератора |
Проверяемое значение частоты f |
действительное значение
|
b ед. |
|
|
|
Тип и номер частомера |
|
Г3-112 |
1 МГц |
0.99 МГц |
36 |
1030 |
362 |
724 |
43-33 №П11377 |
2. Измерение периода колебаний
При измерении низких частот с высокой точностью требуется большое время измерения. Поэтому вместо частоты рекомендуется измерять период колебаний период колебаний Т.
|
№, п/п |
|
|
|
№, п/п |
|
|
|
Примечание |
|
1 |
20.4165 |
-16 |
26 |
20.4025 |
-156 |
|
||
|
2 |
20.4245 |
64 |
27 |
20.4157 |
-24 |
|||
|
3 |
20.4355 |
174 |
28 |
20.4057 |
-124 |
|||
|
4 |
20.4245 |
64 |
29 |
20.4268 |
87 |
|||
|
5 |
20.4045 |
-136 |
30 |
20.4200 |
19 |
|||
|
6 |
20.4000 |
-181 |
31 |
20.4275 |
94 |
|||
|
7 |
20.4261 |
80 |
32 |
20.4245 |
64 |
|||
|
8 |
20.4255 |
74 |
33 |
20.4000 |
181 |
|||
|
9 |
20.4188 |
7 |
34 |
20.4177 |
-4 |
|||
|
10 |
20.4500 |
319 |
35 |
20.4246 |
65 |
|||
|
11 |
20.4355 |
174 |
36 |
20.4117 |
-64 |
|||
|
12 |
20.4057 |
-124 |
37 |
20.4116 |
-65 |
|||
|
13 |
20.4000 |
-181 |
38 |
20.3745 |
-436 |
|||
|
14 |
20.4057 |
-124 |
39 |
20.4280 |
99 |
|||
|
15 |
20.4000 |
-181 |
40 |
20.4025 |
-156 |
|||
|
16 |
20.4356 |
175 |
41 |
20.4037 |
-84 |
|||
|
17 |
20.4077 |
-104 |
42 |
20.4350 |
169 |
|||
|
18 |
20.4355 |
177 |
43 |
20.4355 |
174 |
|||
|
19 |
20.4198 |
17 |
44 |
20.4077 |
-104 |
|||
|
20 |
20.4375 |
194 |
45 |
20.4125 |
-56 |
|||
|
21 |
20.4165 |
-16 |
46 |
20.4355 |
174 |
|||
|
22 |
20.4001 |
-180 |
47 |
20.4065 |
-116 |
|||
|
23 |
20.4157 |
-24 |
48 |
20.4275 |
94 |
|||
|
24 |
20.4275 |
94 |
49 |
20.4157 |
-24 |
|||
|
25 |
20.4255 |
74 |
50 |
20.4335 |
154 |
|||
|
|
5010.4942 |
10020.9066 |
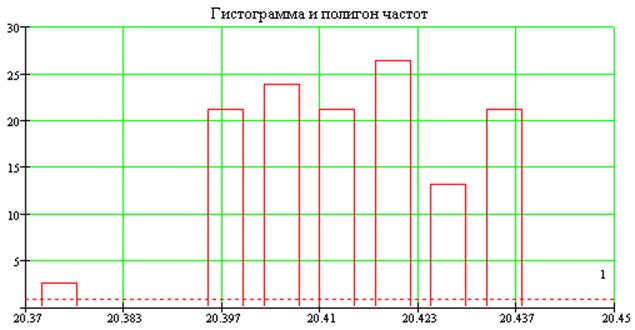
Аппроксимацию
произведем равномерным законом распределения, из равномерного закона
распределения известно что параметр стандартной аппроксимации равен 1.7. Отсюда
оценка среднеквадратичного отклонения результатов наблюдений равняется: 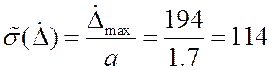
Оценка
среднеквадратического отклонения результата наблюдений: 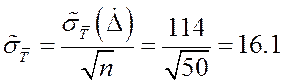 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.