Определение статистических погрешностей измерений, страница 2

Вывод: в результате поверки генератора сигналов низкочастотного Г3-1 образцовым электронносчетным частотомером Ч3-3             , погрешность которого на поверяемой частоте составляет 0,00013 %, в соответствие с приведенной выше таблицей поверки, установлено, что генератор сигналов исправен и разметка его шкалы соответствует допустимой точности (погрешность показаний составляет 0,43%).

2. Измерение периода колебаний с повышенной точностью

2.1. Обработка результатов наблюдений при нормальном

законе распределения случайных отклонений

Табл.4. Измерение периода при нормальном законе

распределения случайных отклонений

i	Т, с	, мкс	, мкс2
1	0,020262	-3,8	14,44
2	0,020268	2,2	4,84
3	0,020263	-2,8	7,84
4	0,020270	4,2	17,64
5	0,020265	-0,8	0,64
6	0,020266	0,2	0,04
7	0,020264	-1,8	3,24
8	0,020263	-2,8	7,84
9	0,020264	-1,8	3,24
10	0,020270	4,2	17,64
11	0,020266	0,2	0,04
12	0,020268	2,2	4,84
13	0,020265	-0,8	0,64
14	0,020270	4,2	17,64
15	0,020263	-2,8	7,84

Проверим правильность расчетов:  с. Расчеты верны.

Оценка СКО результатов наблюдений: 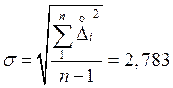 мкс.

Лист 4

         Проверим полученные значения Т_i на наличие промахов. Выберем уровень значимости q = 0,05. При n = 15 выбираем по таблице в методическом пособии ν = 2,49. Наибольшее (наихудшее) значение , значит, промахов нет.

Оценка СКО результата измерения:  мкс.

Определим интервал погрешности измерения с доверительной вероятностью P = 0,95. При этом коэффициент Стьюдента t (n, P) = 2,14.  мкс.

Вывод: в результате эксперимента определили, что Т = 20,2658 мс,  мс, P = 0,95.

2.2. Обработка результатов наблюдений при заранее

неизвестном законе распределения случайных отклонений

Табл.5. Измерение периода при неизвестном законе

распределения случайных отклонений

i	Т, с	i	Т, с	i	T, c	i	T, c	i	T, c
1	20,272	11	20,275	21	20,269	31	20,269	41	20,272
2	20,268	12	20,273	22	20,274	32	20,274	42	20,275
3	20,276	13	20,270	23	20,274	33	20,277	43	20,271
4	20,269	14	20,272	24	20,271	34	20,269	44	20,273
5	20,273	15	20,273	25	20,269	35	20,271	45	20,245
6	20,269	16	20,270	26	20,275	36	20,277	46	20,274
7	20,273	17	20,276	27	20,276	37	20,275	47	20,276
8	20,272	18	20,269	28	20,272	38	20,272	48	20,276
9	20,276	19	20,276	29	20,269	39	20,275	49	20,277
10	20,270	20	20,273	30	20,276	40	20,270	50	20,276

Дальнейшие расчеты производились на ЭВМ. Ниже приведены результаты выполнения программы.

Среднее: Т_ср = 20,273 мс

СКО: σ = 0,002708 с

Рис.1. Гистограмма распределения случайных отклонений

Выберем стандартную аппроксимирующую функцию – нормальную функцию. a = 3,0.

 мс;  мс

Вывод: Т = 20,27 мс, σ_т = 0,223 мс, φ_ст (Δ) – нормальная (усеченная).