Дифференциальный усилитель, состоящий из дифференциального каскада и из генератора стабильного тока (ГСТ), страница 2

При нормальном распределении  параметров вероятности ошибок первого и второго рода при симметричном поле допуска для сигнала [a_i , b_i ]  определяются выражениями:

pnormpnorm,                                   (1)

=   pnorm,                                  (2)

где   – интегральная функция распределения вероятностей в обозначениях программы Mathcad,  – среднее значение (математическое ожидание) параметра ,  - СКЗ сигнала,  - поле допуска, равномерно распределённой аддитивной погрешности .

Для начала запишем допуски на измеряемы параметры:

Δ_Еп=0.01;  Δ_Кu=0.03;  Δ_Rг=0.015;  Δ_Rн=0.15;  Δ_Кпсс=0.015;  Δ_Δf=0.005

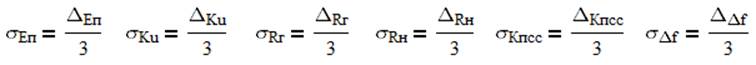
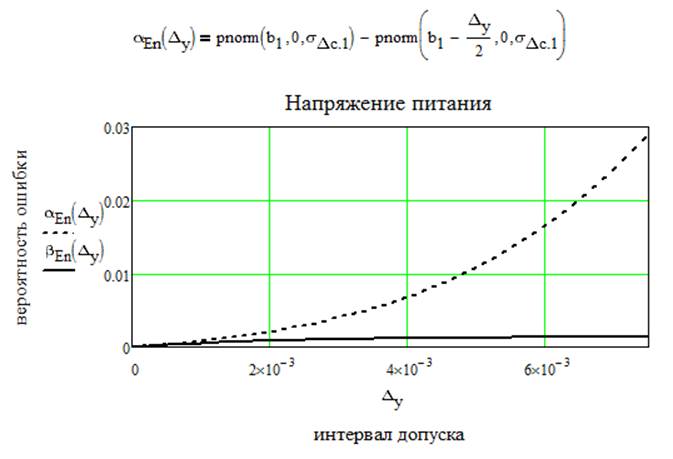
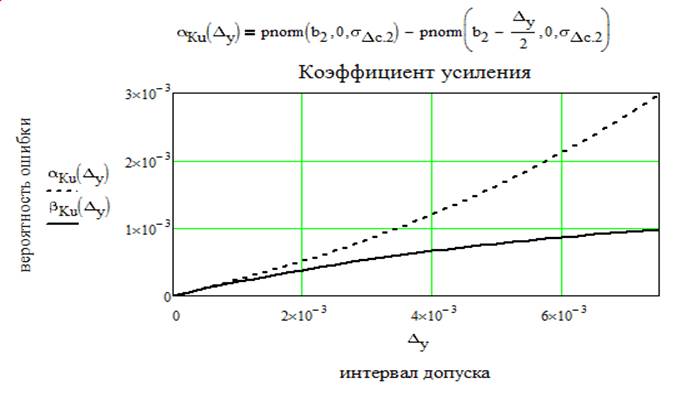
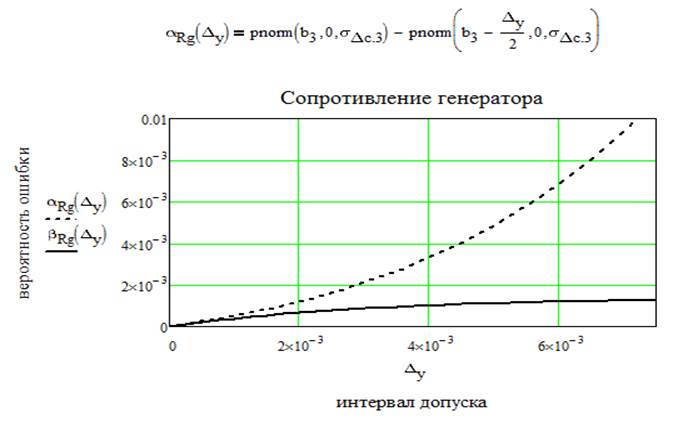
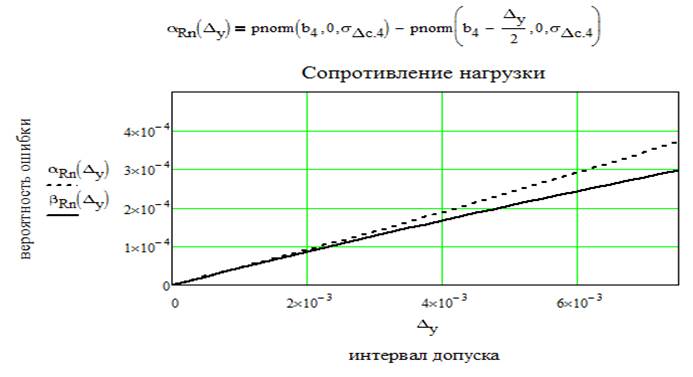
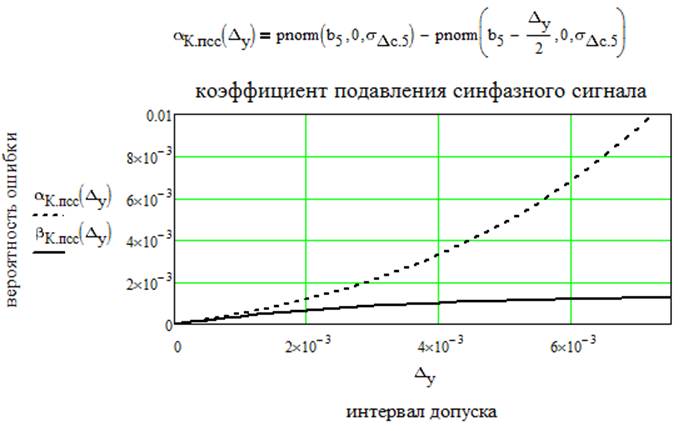
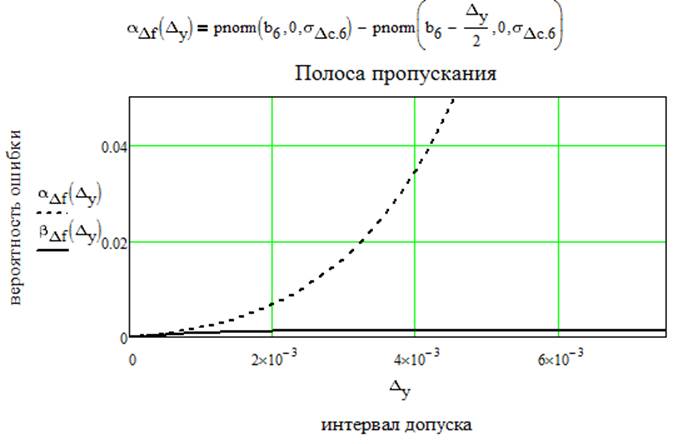
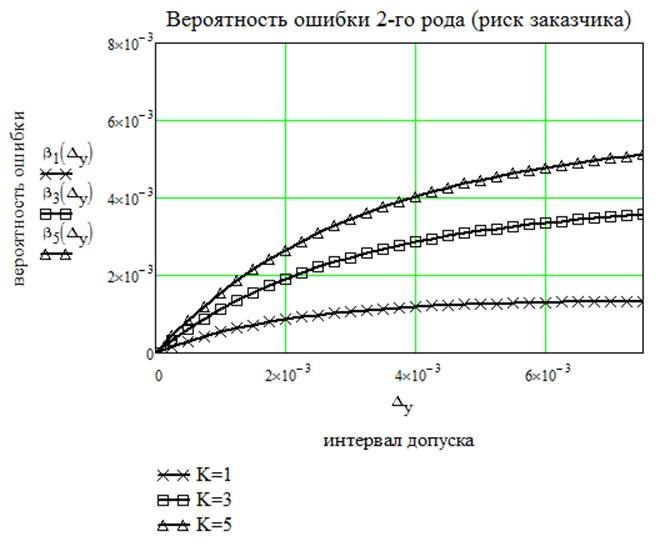
Рассчитаем общие вероятности ошибок первого и второго рода по k контролируемым параметрам и построим зависимости этих ошибок от k. Для расчета воспользуемся следующими формулами:

                                                      (3)

                                                        (4)

Расчеты сделаем по следующему числу контролируемых параметров:

k=1 (1 контролируемый параметр из 7);

k=3 (3 контролируемых параметра из 7);

k=5 (5 контролируемых параметров из 7);

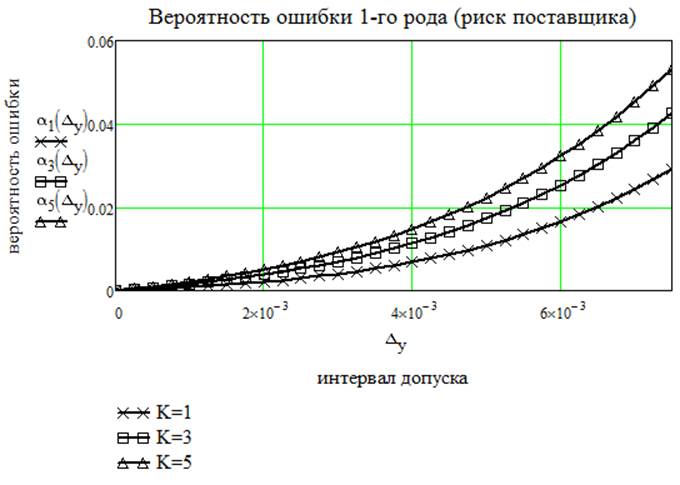
5.  Рассчитаем и построим зависимость суммарных затрат.

Определим функцию суммарных затрат на измерения, потери качества измерений и на брак неконтролируемых параметров. В данной курсовой работе применим следующую модель суммарной функции затрат, которуюпредставим  в следующем виде:

    (5)           

В данном выражении первое слагаемое определяет затраты на измерения k из n параметров объекта контроля, второе и третье  определяют затраты из-за потерь качества измерений, вследствие ошибок первого и второго рода  и четвёртое определяет потери на брак для  неконтролируемых параметров.

 – затраты на измерения k параметров одного изделия,

и - коэффициенты затрат (денежные эквиваленты) на потери из-за ошибок первого и второго рода при измерении k из  n параметров,

;  - общие вероятности ошибок первого и второго рода по k контролируемым параметрам,

Четвертое слагаемое не будем принимать во внимание при расчетах, так как в данной работе проводятся измерения по всем контролируемым параметрам (шесть параметров из шести).

Затраты на измерения k параметров одного изделия  определяются следующим выражением:

 , где                                         (6)

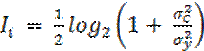 – количество информации (в битах), получаемое при измерении i – того параметра для измерительного канала с аддитивным гауссовым шумом;

 и   - среднеквадратические значения (СКЗ)  измеряемого параметра  и аддитивной погрешности  y;

 – коэффициент затрат на получение одного бита информации  при измерении одного параметра, [];

 ;

Найдем количество информации (в битах), получаемое при измерении каждого параметра:

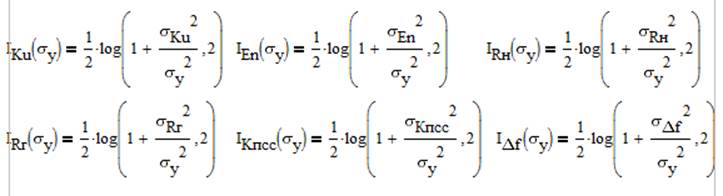
Назначим коэффициенты затрат на получение одного бита информации  при измерении каждого параметра:

K_IKu=10;  K_IEn=12;  K_IRн=18;  K_IRг=15;  K_IKпсс=20;  K_IΔf=100

На практике затраты на потери из-за ошибки второго рода (риска заказчика) как правило гораздо существеннее потерь вызванных ошибкой первого рода (риска поставщика). Назначим коэффициенты затрат (денежные эквиваленты) на потери из-за ошибок первого и второго рода при измерении k из  n параметров:

;   ;

Итак, теперь можно записать суммарные функции затрат для каждого параметра и построить графики.

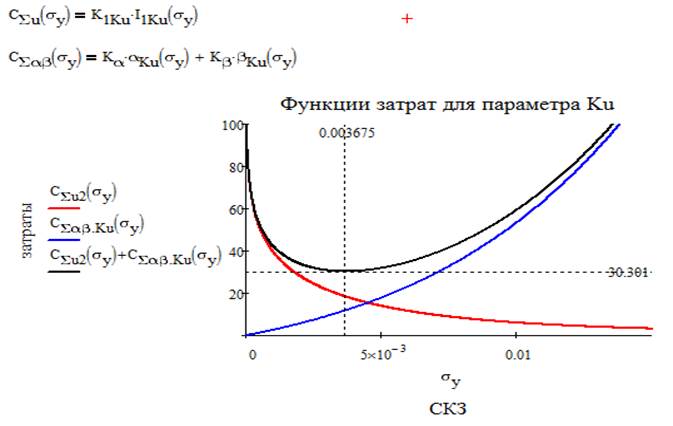
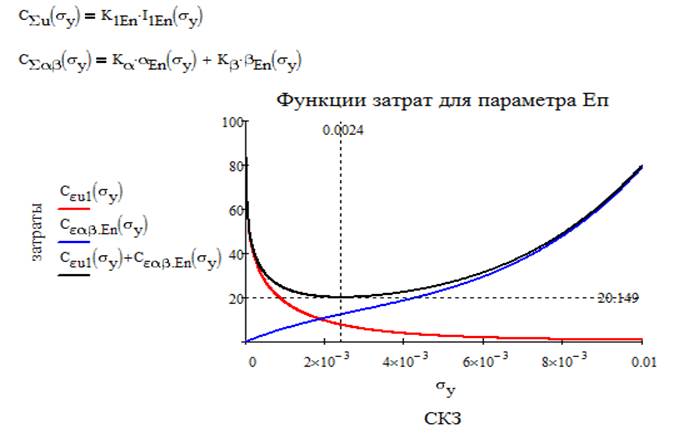
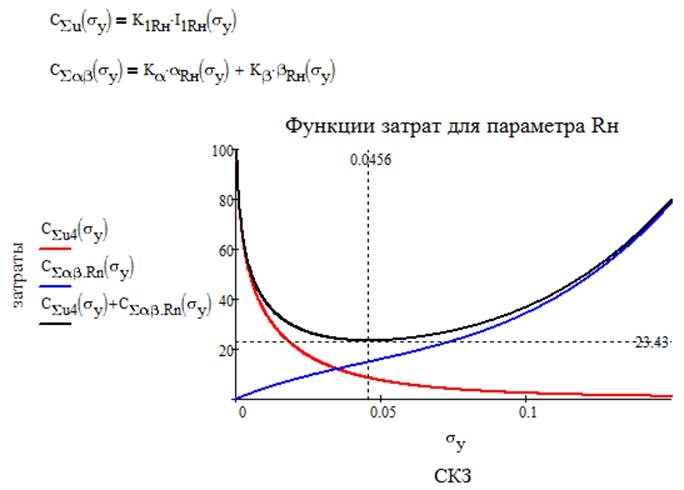
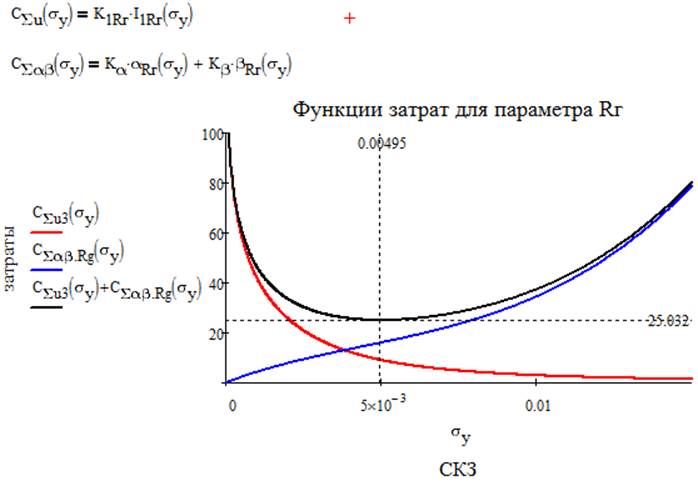
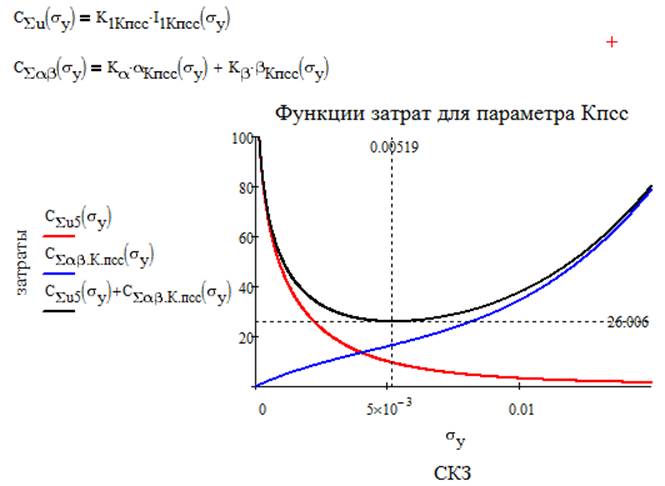
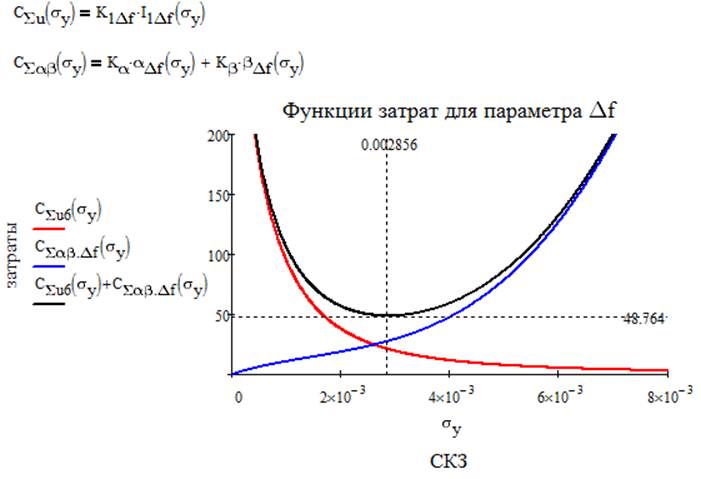
Получаем суммарную функцию затрат на весь объект исследования:

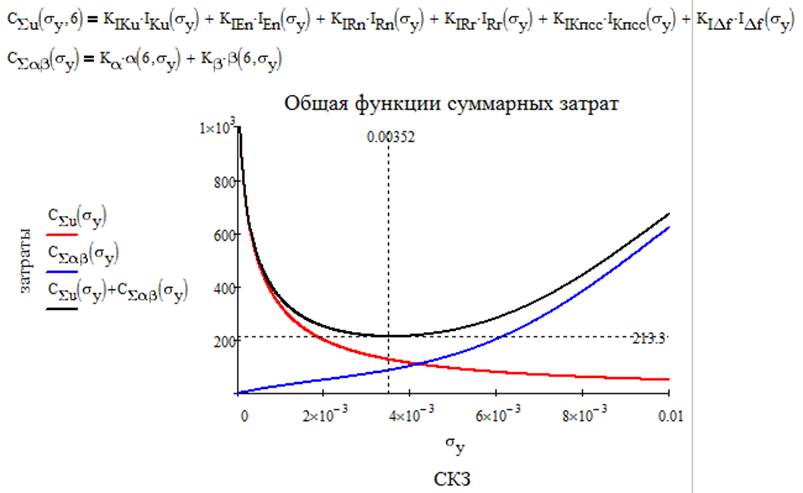
6.  По требуемой величине СКЗ погрешности определить класс точности средства измерения по каждому параметру и выбрать конкретный тип измерительного прибора.

σ_yKu=0.0036;   σ_yEn=0.0024;   σ_yRn=0.0456;  

σ_yRg=0.0049;   σ_yKпсс=0.005;   σ_yΔf=0.0028;  

Для измерения контролируемых параметров нам необходимы такие измерительные приборы, как: вольтметр, частотомер и омметр. Класс точности данных приборов должен удовлетворять величине СКЗ погрешности измерения по каждому параметру для получения качественных результатов. Для данной курсовой работы я выбрал следующие типы измерительных приборов:

      - 34401AМультиметр Agilent Technologies

- цифровой омметр 7556;

- частотомер FLUKE РМ 6685;

Описание приборов:

34401A Мультиметр Agilent Technologies