Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарных электрических и магнитных рамок (витков)

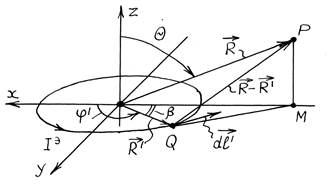
Рис. 1.7

Разместим точку наблюдения  произвольно в окружающем виток пространстве. Как известно [4, 6], решение неоднородного векторного уравнения Гельмгольца

относительно магнитного векторного потенциала  электрического тока в общем случае имеет вид

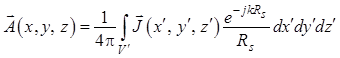, . (1.106)

Это решение для излучателя рис. 1.7 может быть упрощено, если учесть, что ток проводимости (1.105) имеет составляющую только по орту , т. е. по касательной к окружности рамки. В декартовой системе координат такая ориентация тока в витке описывается векторным дифференциалом длины  и уравнение (1.106) для бесконечно тонкого витка принимает вид

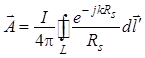,                               (1.107)

где  есть вектор, совпадающий по направлению с током  (уравнение (1.105)) на отрезке витка  (эта величина уже скалярная),  есть расстояние между точкой искомого поля  и элементом тока (рис. 1.7). Преобразуем последнее уравнение к более удобному виду, опираясь на материалы работы [4].

Векторный дифференциал длины , используя рис. 1.8, разложим на две компоненты:

,  (1.108)

где учтено, что , а оба орта  относятся к проекции  точки наблюдения  на плоскость витка . При этом орт  всегда лежит в плоскости витка и в общем случае не является ортом  сферической системы координат, направленным по радиусу-вектору  точки наблюдения . Таким образом, становится ясно, что, поскольку интеграл (1.107) есть вектор, интегрирование есть, по сути дела, сложение множества элементарных векторов, расположенных в различных точках пространства.

Рис. 1.8

При суммировании таких векторов их нужно прежде всего перенести параллельно самим себе в некоторую общую произвольную точку пространства – так называемую «точку приведения», и лишь затем сложить по правилу суммирования векторов (т. е. просуммировать проекции всех элементарных векторов на одноименную ось координат). В прямоугольной декартовой системе координат компоненты любого вектора при параллельном переносе не изменяются. В сферической же системе координат, хотя и являющейся ортогональной системой, правило параллельного переноса более сложное.

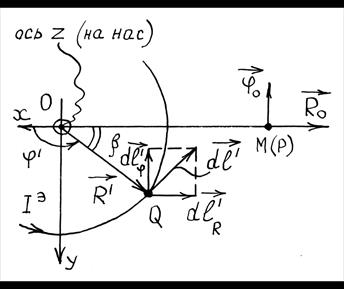
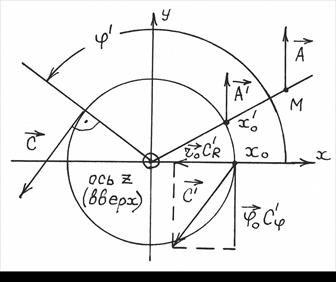
Пусть, например, некоторый вектор  лежит в плоскости  (рис. 1.9) и характеризуется лишь компонентой :

; .     (1.109)

При параллельном переносе этого вектора, например в точку   (рис. 1.9), его компоненты по угловой координате  изменяются и, кроме того, появляется компонента по орту :

; ; .      (1.110)

Рис. 1.9

Как указывалось, выбор точки приведения векторов при их суммировании несуществен и результат сложения не зависит от этого выбора. Однако полученный в результате сложения (интегрирования) итоговый вектор определяется своими компонентами и эти компоненты относятся к выбранной точке и только к ней.

Возвращаясь к нашей задаче и точке наблюдения , естественно принять, что при вычислении компонент векторного потенциала  [формула (1.6.3)] именно точка наблюдения является одновременно и точкой приведения. Поэтому все расположенные на витке элементарные векторы естественно перенести именно в эту точку . Если учесть, что виток расположен в плоскости  (в этой плоскости угол ), то векторный потенциал  в точке  параллелен этой плоскости и имеет те же компоненты в сферических координатах, которые он имел бы, если бы располагался в точке , являющейся проекцией точки  на плоскость  (рис. 1.8). Полученные при этом компоненты вектора  будут равны компонентам этого вектора  в точке . Если теперь из точки переместиться в точку , лежащую на пересечении отрезка ОМ и витка с током (рис. 1.9), то с учетом выражений (1.110) можно записать:

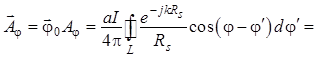
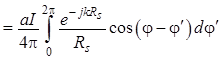,                       (1.111)

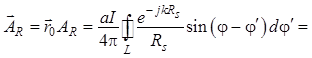
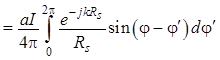,                       (1.112)

,                                   (1.113)

причем расстояние  между рассматриваемыми элементами витка с током и точкой  наблюдения поля

.                     (1.114)

Для дальней зоны Фраунгофера  и последнее выражение можно разложить в ряд:

,                      (1.115)

,                   (1.116)

где

.                                     (1.117)

Тогда формулы (1.111) и (1.112) примут вид

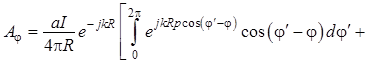
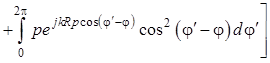,                  (1.118)

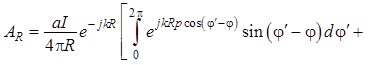
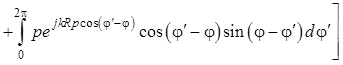.           (1.119)

В последнем выражении необходимо проинтегрировать произведение  на  (здесь ) в пределах от () до (). Такой интеграл равен нулю, и поэтому

.                                  (1.120)

Формула (1.118) для проекции  векторного потенциала примет вид

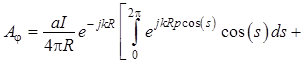
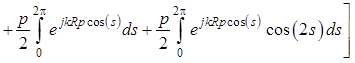.          (1.121)

Напомним, что интеграл

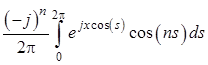,              (1.122)

есть функция Бесселя го порядка, обозначаемая как . Поэтому

,  (1.123)

где

.                        (1.124)

Для нашего случая

, ,                                  (1.125)

и мы можем разложить функции Бесселя в ряды по степеням переменной :

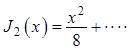; ;  .       (1.126)

В этих рядах все слагаемые, содержащие переменную  во второй и более высоких степенях, малы, и ими можно пренебречь, что и отражено многоточием в последней формуле. Тогда функция Бесселя  второго порядка, определяющее слагаемое, пропорциональное величине , не войдет в выражение (1.123) для компоненты  векторного потенциала. Таким образом, приходим к формуле:

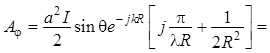
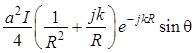 .   (1.127)

Пренебрегая в последнем выражении слагаемым , получаем адекватную оценку потенциала  рамки с током проводимости для точек дальней зоны Фраунгофера:

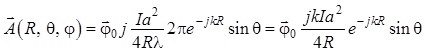.   (1.128)

Теперь определяем составляющие поля излучения рамки. Для магнитного поля имеем:

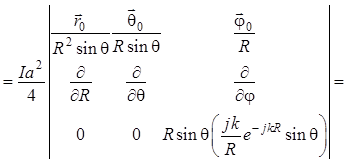
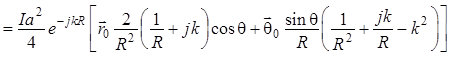. (1.129)

Вновь пренебрегаем слагаемыми, содержащими множители и , и окончательно получаем оценку комплексной амплитуды векторной напряженности магнитного поля излучения рамки:

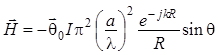.                        (1.130)

Из первого уравнения Максвелла для среды без источников имеем:

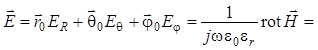
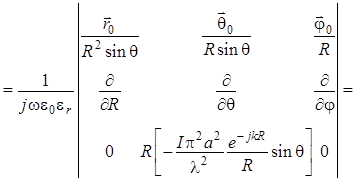
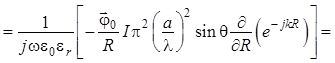
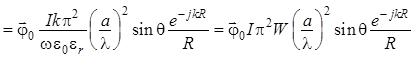.    (1.131)

Таким образом, электромагнитное поле элементарной электрической рамки в дальней зоне Фраунгофера характеризуется следующими составляющими:

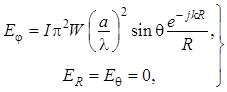                       (1.132)

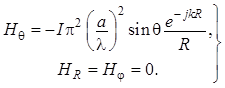                       (1.133)

Сопоставление формул (1.128), (1.129) для магнитного диполя и (1.132), (1.133) для элементарной электрической рамки показывает, что структура электромагнитного поля обоих элементарных излучателей идентична. Отличие в знаках устраняется изменением направлений тока либо в рамке, либо в диполе, а отсутствие множителя () в последних двух формулах (1.132) и (1.133) непринципиально. Это открывает широкие перспективы при разработке конструкций антенн, о чем подробно сообщается в курсе лекций.

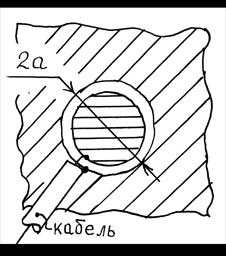
Рис. 1.10

Аналогично может быть установлена идентичность электромагнитного поля электрического диполя Герца и элементарной магнитной рамки, в качестве которой можно использовать узкую кольцевую щель радиусом , сформированная на односторонне фольгированном тонком листе диэлектрика (рис. 1.10). Такая щель возбуждается коаксиальным кабелем, оплетка которого припаивается к внешней, а жила – к внутренней кромке щели. В результате в щели создается радиально направленное электрическое поле, что, согласно принципу эквивалентности, обусловливает существование в щели виртуального кольцевого магнитного тока постоянной амплитуды. Отсюда и название излучателя – элементарная магнитная рамка.