После подбора коэффициентов связи ответвителей первой линии, установки соответствующих фазосдвигателей и подбора их фазовых сдвигов (иными словами, после формирования положения в пространстве первого луча многолучевой ФАР) можно переходить к рассмотрению следующего луча, формируемого со второго входа. Ясно, что подобранные параметры ответвителей и фазосдвигателей первой линии передачи (первого луча) далее не должны изменяться до тех пор, пока не будет признано целесообразным изменить характеристики (уровень боковых лепестков и/или угол отклонения от направления в зенит) первого луча.
Итак, пусть теперь антенна питается со второго входа (![]() ). Тогда в отсутствие фазосдвигателей
возбуждение излучателей характеризуется следующими комплексными амплитудами при
входном напряжении
). Тогда в отсутствие фазосдвигателей
возбуждение излучателей характеризуется следующими комплексными амплитудами при
входном напряжении ![]() :
:
а) для первого излучателя (один путь передачи сигнала):
![]() , (11)
, (11)
б) для второго излучателя (два пути передачи сигнала):
![]() , (12)
, (12)
в) для третьего излучателя (три пути передачи сигнала):
![]()
![]() , (13) и
так далее. Как видно, даже без фазосдвигателей уравнения для напряжений на излучателях
со второго входа получаются весьма громоздкими. К тому же, изменять параметры
, (13) и
так далее. Как видно, даже без фазосдвигателей уравнения для напряжений на излучателях
со второго входа получаются весьма громоздкими. К тому же, изменять параметры ![]() первой «линейки» ответвителей уже нельзя,
так как они определяют положение первого луча ФАР. Поэтому можно подбирать лишь
параметры
первой «линейки» ответвителей уже нельзя,
так как они определяют положение первого луча ФАР. Поэтому можно подбирать лишь
параметры ![]() второй «линейки» ответвителей так, чтобы
обеспечить требуемое распределение амплитуд и фаз возбуждения вдоль излучателей.
Существенно то, что теперь исходя из положения в пространстве второго луча (т.
е. исходя из его уровня боковых лепестков и отклонения максимума диаграммы
направленности) необходимо подбирать коэффициенты связи второй «линейки»
ответвителей и величины задержек фазосдвигателей во второй линии передачи и/или
между второй и первой линиями совместно, так как в уравнениях (12),
(13) производится, фактически, векторное суммирование. Поэтому анализ и
проектирование матриц Бласса представляет собой трудоемкую задачу, которую
можно решить для конкретных чисел М и N только методами
нелинейной параметрической оптимизации.
второй «линейки» ответвителей так, чтобы
обеспечить требуемое распределение амплитуд и фаз возбуждения вдоль излучателей.
Существенно то, что теперь исходя из положения в пространстве второго луча (т.
е. исходя из его уровня боковых лепестков и отклонения максимума диаграммы
направленности) необходимо подбирать коэффициенты связи второй «линейки»
ответвителей и величины задержек фазосдвигателей во второй линии передачи и/или
между второй и первой линиями совместно, так как в уравнениях (12),
(13) производится, фактически, векторное суммирование. Поэтому анализ и
проектирование матриц Бласса представляет собой трудоемкую задачу, которую
можно решить для конкретных чисел М и N только методами
нелинейной параметрической оптимизации.
1.2.2. Параллельное ДОУ, называемое еще матрицей
Батлера (по фамилии зарубежного исследователя ФАР – Butler), может быть реализовано
лишь для чисел ![]() – целое число. В этом ДОУ
отсутствуют балластные резисторы, КПД всех лучей равны
100 % и СВЧ сигнал от каждого входа ФАР поступает к излучателям по схеме
двоично-этажного питания (т. е. по схеме «елочка»). При этом ДОУ содержит
однотипные полосковые или микрополосковые мосты (т. е. направленные
ответвители с коэффициентом связи
– целое число. В этом ДОУ
отсутствуют балластные резисторы, КПД всех лучей равны
100 % и СВЧ сигнал от каждого входа ФАР поступает к излучателям по схеме
двоично-этажного питания (т. е. по схеме «елочка»). При этом ДОУ содержит
однотипные полосковые или микрополосковые мосты (т. е. направленные
ответвители с коэффициентом связи ![]() ) и фазосдвигатели.
Структурные схемы ДОУ на 4 и 8 лучей представлены на рис. 6.
) и фазосдвигатели.
Структурные схемы ДОУ на 4 и 8 лучей представлены на рис. 6.
Рассмотрим особенности работы 4-лучевой матрицы
Батлера на центральной частоте ![]() . В этом случае
. В этом случае
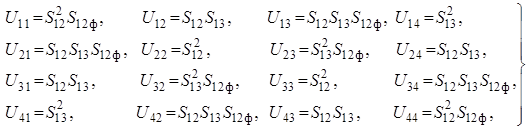 (14)
(14)
и
с учетом (2) и (5) можно констатировать, что сигнал делится поровну между
излучателями, т. е. амплитудное распределение возбуждения вдоль излучателей
равномерное ![]() и уровень боковых лепестков для каждого из
четырех лучей составляет «минус» 13 дБ.
В то же время фазовое распределение возбуждения
и уровень боковых лепестков для каждого из
четырех лучей составляет «минус» 13 дБ.
В то же время фазовое распределение возбуждения ![]()
![]() для каждого входа является линейно изменяющимся
(рис. 7), причем в формуле (2)
для каждого входа является линейно изменяющимся
(рис. 7), причем в формуле (2) ![]() , а разности фаз (9) и
углы отклонения (10) составят:
, а разности фаз (9) и
углы отклонения (10) составят:
а) первый луч, ![]() ,
,
![]() ,
, ![]() вправо
от нормали, (15)
вправо
от нормали, (15)
б) второй луч, ![]() ,
,
![]() ,
, ![]() влево от
нормали, (16)
влево от
нормали, (16)
в) третий луч, ![]() ,
,
![]() ,
, ![]() вправо
от нормали, (17)
вправо
от нормали, (17)
г) четвертый луч, ![]() ,
, ![]() ,
, ![]() влево от нормали. (18)
влево от нормали. (18)
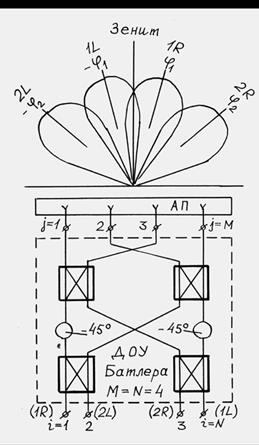
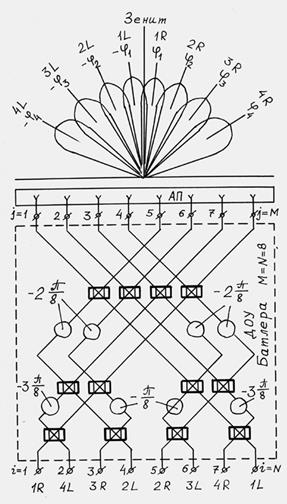
а б
Рис. 6
Таким образом, 1-й и 3-й лучи отклонены вправо от
направления в зенит (на рис. 6, a введено дополнительное
обозначение 1R, 2R; буква «R» от слова «Right» – правый), а второй и
четвертый – влево
(на рис. 6, а дополнительные обозначения 1L, 2L;
буква «L» от слова «Left» – левый). При этом
целесообразно подчеркнуть, что на рис. 7 некоторые значения ![]() для второго и третьего лучей изменены на
для второго и третьего лучей изменены на ![]() и фазовое распределение продолжено
штриховыми линиями.
и фазовое распределение продолжено
штриховыми линиями.
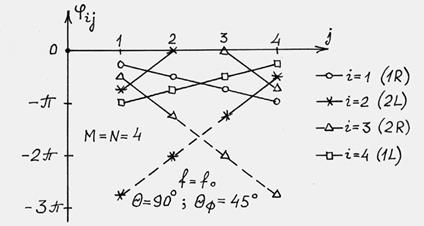
Рис. 7
Матрица Батлера с числом лучей 8 работает аналогично. При этом разности фаз и углы отклонений лучей составляют:
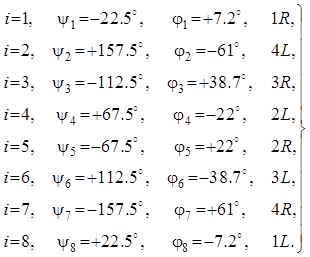 (19)
(19)
1.2.3. Комбинированное
ДОУ, называемое ещё матрицей Нолена (по фамилии зарубежного исследователя –
Nolen), реализуется для любых чисел ![]() также без балластных
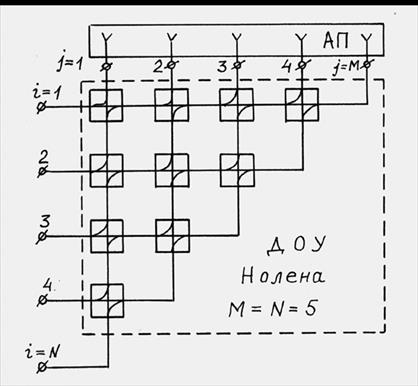
резисторов и имеет 100-процентный КПД по каждому лучу. В качестве примера на
рис. 8 представлена матрица Нолена для
также без балластных
резисторов и имеет 100-процентный КПД по каждому лучу. В качестве примера на
рис. 8 представлена матрица Нолена для ![]() (без
фазосдвигателей).
(без
фазосдвигателей).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.