Анализ и синтез автомата Мили в базисе “ИЛИ-НЕ” на синхронных RS-тригерах

Министерство образования Российской Федерации

Хабаровский государственный Технический Университет

Курсовая работа

По курсу:

“Теория автоматов”

на тему:

“Анализ и синтез автомата Мили”

Выполнил: Мутаев А.А.

Группа ВМ^У шифр: 0013373

Хабаровск

2001г

Задание.

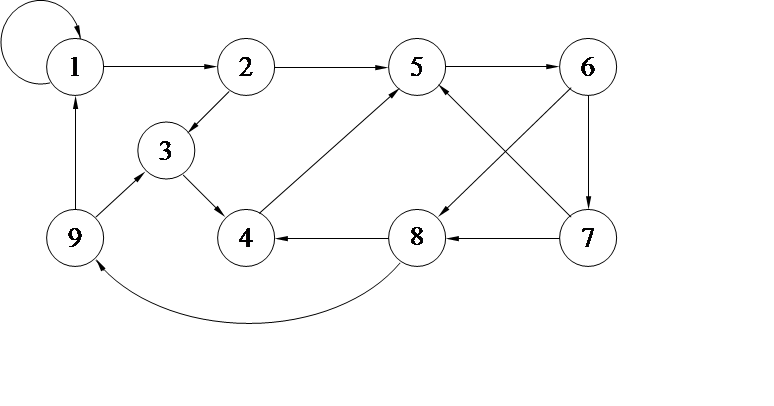
Синтезировать цифровой автомат по заданному графу в базисе ИЛИ-НЕ на D- или RS- тригерах.

1/1

2/2                               1/2                               2/2          

2/1                                                      1/2        1/1

2/1

2/2                                                                                                               2/1

1/1                   2/2

1/2                               2/2

2/1

Анализ цифрового автомата Мили.

Общие понятия и сведения из теория.

Алгоритм работы автомата описывается автоматными отображениями.

Таблица переходов (выходов) представляет собой таблицу с двумя значениями, строки которой нумерованны из алфавита входных (выходных) сообщений, а столбцы – состояниями. На пересечении указывается состояние, в которое переходит автомат (или выходной сигнал), при поступлении на вход сигнала указанного в левом столбце.

Zi+1 Yi

Zi	Z0	Z1	,,,,,,	,,,,,,	,,,,,,,	Zk
Xi
X1
, ,
Xn

Рис 1.1

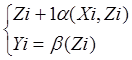 - Автомат Мили

Эти таблицы удобны для машинного и ручного синтеза. Но по ним трудно вести анализ автомата.

Процедура анализа обычно предшествует синтезу ЦА и включает в себя:

1.  Анализ рабоспособности.

2.  Возможность разбиения автомата на подавтоматы.

3.  Минимизация состояний автомата.

Часто автомат задают с помощью графа. Граф автомата – ориентированный граф вершины которого соответстуют состояниям, а дуги – переходам между ними.

Xi/Yi

 

Для автомата Мили

По графу автомата определяется возможность разбиения на подавтоматы, с целью упрощения дальнейшей минимизации и синтеза автомата.

Различают:

А) Изолированные подавтоматы.

Это ситуация, при которой группа вершин гафа автомата не имеет никаких связей с другими вершинами.

Б) Тупиковые подавтоматы.

Это ситуация, при которой подавтоматы не содержат исходящих дуг.

В) Переходящие автоматы.

Это ситуация, при которой подавтомат образуется вершинами,  имеющими только исходящие дуги.

Для удобства построения составим таблицу переходов- выходов.

Zi Xi	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
X1	Z1 Y1	Z5 Y2				Z8 Y1	Z5 Y2	Z4 Y2	Z3 Y1
X2	Z2 Y2	Z3 Y1	Z4 Y2	Z5 Y1	Z6 Y2	Z7 Y1	Z8 Y2	Z9 Y1	Z1 Y2

Кодирование состояний цифрового автомата Мили.

Результатом канонического структурного синтеза является система канонических (логических выражений для выходных Yi и сигналов функций возбуждения памяти Zi+1 в зависимости от входных Xi и состояний памяти Zi) уравнений.

С учетом кодирования можно записать:

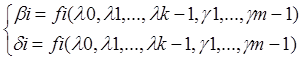
i=0,1,2,…,m-1

Сложность реализации оценивается по Квайну и зависит от способов кодировки состояний автомата: . Сформулируем правило Баранова (1979): При использовании элементов памяти на тригерах с раздельными входами, нужно применять критерий минимизации элементарных переходоа тригеров. Это приводит к соседнему кодированию. Минимизация происходит по суммарному кодовому расстоянию между кодами возможных переходов.

Для оценки эффективности двух различных кодировок подсчитывают число переходов из Zi в Zi+1 и сумму кодовых расстояний для всех этих переходов, при этом учитываются кратные и противоположные дуги и не учитываются петли.

Коэффициент эффективности:

К_эф=L/N ; где

L – суммарное кодовое расстояние

N – Количество переходов

Средний коэффициент эффективности кодирования должен лежать в пределах 1.4≤К_эф≤2.1. Для чистого кода Грея К_эф=1. Для упрощения КС автомата, снижения его цены по Квайну и в целях снижения трудоемкости по выполнению задания найдем оптимальный вариант кодирования.

Подсчитаем коэффициент эффективности обычного двоичного кода и модифицированного кода.

Zi	1способ				2способ
	δ3	δ2	δ1	δ0	δ3	δ2	δ1	δ0
Z1	0	0	0	0	1	1	1	0
Z2	0	0	0	1	0	1	0	0
Z3	0	0	1	0	0	0	1	0
Z4	0	0	1	1	0	0	1	1
Z5	0	1	0	0	0	0	0	0
Z6	0	1	0	1	0	0	0	1
Z7	0	1	1	0	0	1	0	1
Z8	0	1	1	1	0	1	1	1
Z9	1	0	0	0	0	1	1	0
	Кэф=1.64				Кэф=1.36