Проектирование принципиальной схемы процессора для вычисления функции sin(j) методом «цифра за цифрой», страница 2

На втором этапе на основании найденного в предыдущем этапе набора значений операторов x_i определяется величина вычисляемой элементарной функции. Это выполняется либо путем суммирования слагаемых одного из видов: , причем i-е слагаемое соответствует i-му члену произведения первого этапа, либо с помощью вычисления произведения действительных  или комплексных  чисел, в котором i-ый член произведения соответствует i-му слагаемому, используемому на первом этапе.

Каждый этап вычисления выполняется за n шагов  и представляет собой итерационный процесс, состоящий в построении последовательности: . Обозначив разность между двумя соседними членами последовательности: , назовем данную величину шагом итерации. Каждая итерация первого этапа состоит в определении знака оператора x_i на основании d_i. На каждой итерации второго этапа определяется второй член последовательности u_i, сходящейся к вычисляемой элементарной функции.

2.1.Рекурентные соотношения метода «цифра за цифрой»

Алгоритмы вычисления элементарных функций по методу «цифра за цифрой» могут быть представлены в виде рекуррентных соотношений, содержащих только операции сдвига и алгебраического сложения. Такая форма записи имеет значительные преимущества при машинной организации. Далее приводятся рекуррентные соотношения для вычисления функций sin(j) и cos(j) по способу Волдера. Способ Волдера является наиболее приемлемым, по сравнению со способом Меджита, так как оба этапа вычисления производятся одновременно и составляют единый процесс. (формулы приведены с учетом основания системы счисления, a=2). [1]

Функции sin(j), cos(j).

Этап I 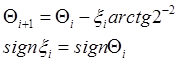                                                                             (1)

Этап II 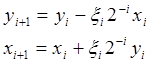                                                                                 (2)

где i=0,1,2, …, n-1

Начальные условия: Q₀=j, у₀=0, х₀=1/K.

Результаты: у_n=-sin(j), x_n=cos(j).

Коэффициент К (коэффициент деформации вектора) вычисляется перед началом использования рекуррентных соотношений по формуле (3).

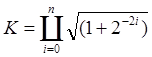                                                 (3)

2.2. Формулы приведения функции sin(j).

Если выделить целую часть I и остаток F от деления j на p/2, то значение sin(j) определяется по формуле (4).

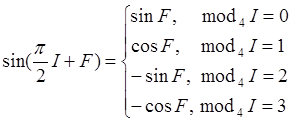                                         (4)

3. Выбор варианта реализации

Как видно из описания вычисления функции sin(j) методом «цифра за цифрой» основными действиями будут являться операции сдвига и алгебраического сложения. Так как основным критерием разработки схемы является оптимизация по быстродействию, то необходимо ускорить операции сдвига и алгебраического сложения.

Наиболее быстрый сдвиг можно получить, используя мультиплексоры. В этом случае удается произвести сдвиг за один такт, но данное решение эффективно использовать при малой разрядности (например 8). С увеличением числа разрядов, на которое необходимо произвести сдвиг, аппаратные затраты неоправданно возрастают.

Для чисел с большой разрядностью (когда число разрядов, на которое необходимо произвести сдвиг заранее не известно, но известны пределы этого числа) сдвиг производят с помощью сдвиговых регистров, при этом время сдвига прямо пропорционально числу разрядов, на которое необходимо произвести сдвиг.

Поэтому для увеличения скорости сдвига, необходимо увеличить частоту на которой производится одиночный сдвиг.

Арифметическое сложение можно реализовать на базе арифметико-логических устройств. Самое быстрое сложение (здесь и далее под сложение подразумевается арифметическое сложение) можно получить, используя арифметико-логическое устройство с параллельным переносом и разрядностью равной заданной разрядности (в данном проекте разрядность =24). Но, исходя из экономических показателей, промышленность выпускает арифметико-логические устройства с разрядностью равной 4.