Содержание:
Задание…………………………………………………………………………………….3
Решение……………...…………………………………………………………………….4
Программа, реализующая решение…...…………………………………………………7
Графическое представление решения...………………………………………………...11
Задание:
Дана
область ![]() :
:
.

На области
![]() найти
найти ![]() удовлетворяющие
условию:
удовлетворяющие
условию: 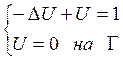
Решение:
Триангулируем
область ![]() с шагом h:
с шагом h:
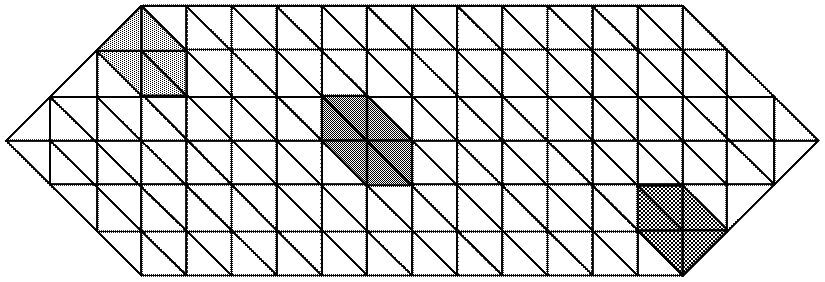
В итоге триангуляции области выделились три конечных элемента:
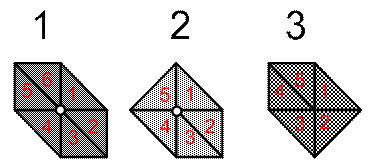
Рассмотрим конечный элемент №1:
Для
того чтобы найти функцию, которая описывает эту область, необходимо найти все
функции ![]() , вида
, вида ![]() ,
описывающие каждый треугольник этого элемента, для этого для каждого
треугольника решим систему уравнений:
,
описывающие каждый треугольник этого элемента, для этого для каждого
треугольника решим систему уравнений: 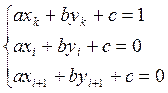 ,
относительно a,b,c.
,
относительно a,b,c.
В итоге получим: 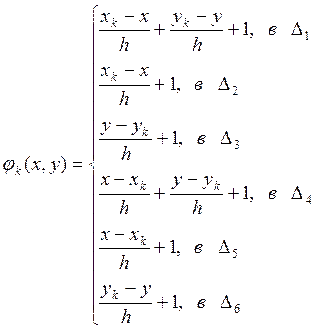 ,
,
так же найдем 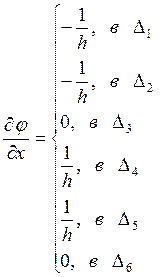 и
и 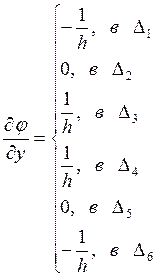
Далее
из уравнения: 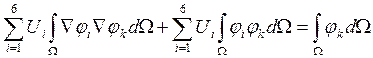 , выражаем
, выражаем ![]() ,
,
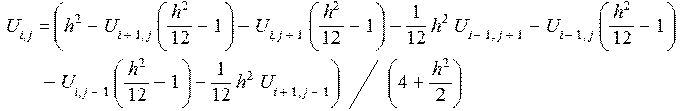
Рассмотрим конечный элемент №2:
Для
того чтобы найти функцию, которая описывает эту область, необходимо найти все
функции ![]() , вида
, вида ![]() ,
описывающие каждый треугольник этого элемента, для этого для каждого
треугольника решим систему уравнений:
,
описывающие каждый треугольник этого элемента, для этого для каждого
треугольника решим систему уравнений: 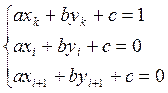 ,
относительно a,b,c.
,
относительно a,b,c.
В итоге получим: 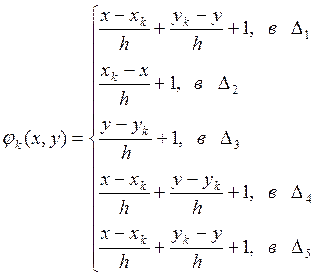 ,
,
так же найдем 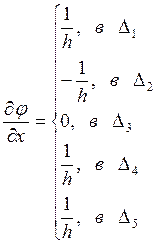 и
и 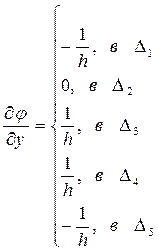
Далее
из уравнения: 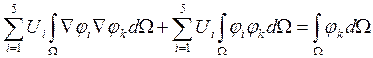 , выражаем
, выражаем ![]() ,
,
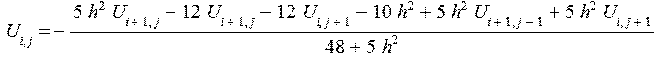
Рассмотрим конечный элемент №3:
Исходя из симметрии области
№2 и №3, уравнение ![]() для области №3, так как
для области №3, так как ![]() ,
, ![]() и
и ![]() для симметричных точек равны, то мы
получим
для симметричных точек равны, то мы
получим
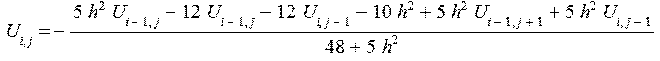
Программа, реализующая решение:
restart;
#Oбласть №1
f11:=(xk-x)/h+(yk-y)/h+1;
df11dx:=diff(f11,x);
df11dy:=diff(f11,y);
f16:=(yk-y)/h+1;
df16dx:=diff(f16,x);
df16dy:=diff(f16,y);
f15:=(x-xk)/h+1;
df15dx:=diff(f15,x);
df15dy:=diff(f15,y);
f14:=(x-xk)/h+(y-yk)/h+1;
df14dx:=diff(f14,x);
df14dy:=diff(f14,y);
f13:=(y-yk)/h+1;
df13dx:=diff(f13,x);
df13dy:=diff(f13,y);
f12:=(xk-x)/h+1;
df12dx:=diff(f12,x);
df12dy:=diff(f12,y);
#Область №2
#Delta 1
sv1:=solve({a*xk+b*yk+c = 1, a*xk+b*(yk+h)+c = 0, a*(xk+h)+b*yk+c = 0}, [a, b, c]):
af:=subs( sv1[1], a );bf:=subs( sv1[1], b );cf:=subs(sv1[1],c);
f21:=expand(af*x+bf*y+cf);
df21dx:=diff(f21,x);
df21dy:=diff(f21,y);
#Delta 2
sv2:=solve({a*xk+b*yk+c = 1, a*(xk+h)+b*yk+c = 0, a*(xk+h)+b*(yk-h)+c = 0}, [a, b, c]):
af:=subs( sv2[1], a );bf:=subs( sv2[1], b );cf:=subs( sv2[1], c );
f22:=expand(af*x+bf*y+cf);
df22dx:=diff(f22,x);
df22dy:=diff(f22,y);
#Delta 3
sv3:=solve({a*xk+b*yk+c = 1, a*xk+b*(yk-h)+c = 0, a*(xk+h)+b*(yk-h)+c = 0}, [a, b, c]):
af:=subs( sv3[1], a );bf:=subs( sv3[1], b );cf:=subs( sv3[1], c );
f23:=expand(af*x+bf*y+cf);
df23dx:=diff(f23,x);
df23dy:=diff(f23,y);
#Delta 4.
sv4:=solve({a*xk+b*yk+c = 1, a*(xk-h)+b*yk+c = 0, a*xk+b*(yk-h)+c = 0}, [a, b, c]):
af:=subs( sv4[1], a );bf:=subs( sv4[1], b );cf:=subs( sv4[1], c );
f24:=expand(af*x+bf*y+cf);
df24dx:=diff(f24,x);
df24dy:=diff(f24,y);
#Delta 5.
sv5:=solve({a*xk+b*yk+c = 1, a*(xk-h)+b*yk+c = 0, a*xk+b*(yk+h)+c = 0}, [a, b, c]):
af:=subs( sv5[1], a );bf:=subs( sv5[1], b );cf:=subs( sv5[1], c );
f25:=expand(af*x+bf*y+cf);
df25dx:=diff(f25,x);
df25dy:=diff(f25,y);
#Градиенты области №2
#fk*fk
#1
gfk1:=simplify(int(int((df21dx^2+df21dy^2),y=yk..yk-x+xk+h),x=xk..xk+h));
#2
gfk2:=simplify(int(int((df22dx^2+df22dy^2),y=yk-x+xk..yk),x=xk..xk+h));
#3
gfk3:=simplify(int(int((df23dx^2+df23dy^2),y=yk-h..yk-x+xk),x=xk..xk+h));
#4
gfk4:=simplify(int(int((df24dx^2+df24dy^2),y=yk-x+xk-h..yk),x=xk-h..xk));
#5
gfk5:=simplify(int(int((df25dx^2+df25dy^2),y=yk..yk+x-xk+h),x=xk-h..xk));
gfk:=gfk1+gfk2+gfk3+gfk4+gfk5;
#f2*fk
#1
gf21:=simplify(int(int((df21dx*df15dx+df21dy*df15dy),y=yk..yk-x+xk+h),x=xk..xk+h));
#2
gf22:=simplify(int(int((df22dx*df14dx+df22dy*df14dy),y=yk-x+xk..yk),x=xk..xk+h));
gf2:=gf21+gf22;
#f3*fk
#2
gf32:=simplify(int(int((df22dx*df16dx+df22dy*df16dy),y=yk-x+xk..yk),x=xk..xk+h));
#3
gf33:=simplify(int(int((df23dx*df15dx+df23dy*df15dy),y=yk-h..yk-x+xk),x=xk..xk+h));
gf3:=gf32+gf33;
#f4*fk
#3
gf43:=simplify(int(int((df23dx*df11dx+df23dy*df11dy),y=yk-h..yk-x+xk),x=xk..xk+h));
#4
gf44:=simplify(int(int((df24dx*df16dx+df24dy*df16dy),y=yk-x+xk-h..yk),x=xk-h..xk));
gf4:=gf43+gf44;
#Интегралы области №2
#fk*fk
#1
pfk1:=simplify(int(int((f21^2),y=yk..yk-x+xk+h),x=xk..xk+h));
#2
pfk2:=simplify(int(int((f22^2),y=yk-x+xk..yk),x=xk..xk+h));
#3
pfk3:=simplify(int(int((f23^2),y=yk-h..yk-x+xk),x=xk..xk+h));
#4
pfk4:=simplify(int(int((f24^2),y=yk-x+xk-h..yk),x=xk-h..xk));
#5
pfk5:=simplify(int(int((f25^2),y=yk..yk+x-xk+h),x=xk-h..xk));
pfk:=pfk1+pfk2+pfk3+pfk4+pfk5;
#f2*fk
#1
pf21:=simplify(int(int((f21*f15),y=yk..yk-x+xk+h),x=xk..xk+h));
#2
pf22:=simplify(int(int((f22*f14),y=yk-x+xk..yk),x=xk..xk+h));
pf2:=pf21+pf22;
#f3*fk
#2
pf32:=simplify(int(int((f22*f16),y=yk-x+xk..yk),x=xk..xk+h));
#3
pf33:=simplify(int(int((f23*f15),y=yk-h..yk-x+xk),x=xk..xk+h));
pf3:=pf32+pf33;
#f4*fk
#3
pf43:=simplify(int(int((f23*f11),y=yk-h..yk-x+xk),x=xk..xk+h));
#4
pf44:=simplify(int(int((f24*f16),y=yk-x+xk-h..yk),x=xk-h..xk));
pf4:=pf43+pf44;
#f*fk
#1
pffk1:=simplify(int(int((f21),y=yk..yk-x+xk+h),x=xk..xk+h));
#2
pffk2:=simplify(int(int((f22),y=yk-x+xk..yk),x=xk..xk+h));
#3
pffk3:=simplify(int(int((f23),y=yk-h..yk-x+xk),x=xk..xk+h));
#4
pffk4:=simplify(int(int((f24),y=yk-x+xk-h..yk),x=xk-h..xk));
#5
pffk5:=simplify(int(int((f25),y=yk..yk+x-xk+h),x=xk-h..xk));
pffk:=pffk1+pffk2+pffk3+pffk4+pffk5;
eqUk2:={gfk*U[i,j]+gf2*U[i+1,j]+gf3*U[i+1,j-1]+gf4*U[i,j+1]+pfk*U[i,j]+pf2*U[i+1,j]+pf3*U[i+
1,j-1]+pf4*U[i,j+1]=pffk};
solv:=solve(eqUk2,U[i,j]);
U2:=(i,j)->-(5*h^2*U[i+1,j]-12*U[i+1,j]-12*U[i,j+1]-10*h^2+5*h^2*U[i+1,j-1]+5*h^2*U[i,j+1])/
(48+5*h^2);
eqUk3:={gfk*U[i,j]+gf2*U[i-1,j]+gf3*U[i-1,j+1]+gf4*U[i,j-1]+pfk*U[i,j]+pf2*U[i-1,j]+pf3*U[i1,j+1]+pf4*U[i,j-1]=pffk};
solv:=solve(eqUk3,U[i,j]);
U3:=(i,j)->-(5*h^2*U[i-1,j]-12*U[i-1,j]-12*U[i,j-1]-10*h^2+5*h^2*U[i-1,j+1]+5*h^2*U[i,j-1])/
(48+5*h^2);
U1:=(i,j)->(1/(4+h^2/2))*(h^2-U[i+1,j]*(h^2/12-1)-U[i,j+1]*(h^2/12-1)-U[i-1,j+1]*h^2/12-U[i1,j]*(h^2/12-1)-U[i,j-1]*(h^2/12-1)-U[i+1,j-1]*h^2/12);
#Решение
h:=0.1:
eps:=0.001:
lx:=round(3/h):ly:=round(1/h):
U:=array(0..lx,0..ly):
for i from 0 by 1 to lx do
for j from 0 by 1 to ly do
U[i,j]:=-1;
end do;
end do;
maxeps:=eps*2:step:=0:
for j while j>0 do
maxeps:=0:step:=step+1:
for i from 0 by 1 to lx do
for j from 0 by 1 to ly do
if (((i<=ly/2)and(j<=(ly/2-i)))or
((i<=ly/2)and(j>=(ly/2+i)))or
((i>=lx-ly/2)and(j>=(ly/2-i+lx)))or
((i>=lx-ly/2)and(j<=(ly/2+i-lx)))or
(j=0)or(j=ly)
)
then
U[i,j]:=0:
else
if ((i-1=ly/2-j)and(i<>0)and(j<>0))
then
Ueps:=U2(i,j):
teps:=abs(Ueps-U[i,j]):
if(teps>maxeps) then maxeps:=teps: end if;
U[i,j]:=Ueps:
else
if ((i-(lx-ly/2-1)=-j+ly)) then
Ueps:=U3(i,j):
teps:=abs(Ueps-U[i,j]):
if(teps>maxeps) then maxeps:=teps: end if;
U[i,j]:=Ueps:
else
Ueps:=U1(i,j):
teps:=abs(Ueps-U[i,j]):
if(teps>maxeps) then maxeps:=teps: end if;
U[i,j]:=Ueps:
end if;
end if:
end if:
end do:
end do:
if(maxeps<=eps) then break; end if;
end do:
Um:=Matrix(lx+1,lx+1):
for i from 1 by 1 to lx+1 do
for j from 1 by 1 to lx+1 do
if ((j>=round(lx/2)-ly/2)and(j<=round(lx/2)+ly/2)) then
Um[i,j]:=U[i-1,j-ly];
else
Um[i,j]:=0;
end if;
end do;
end do;
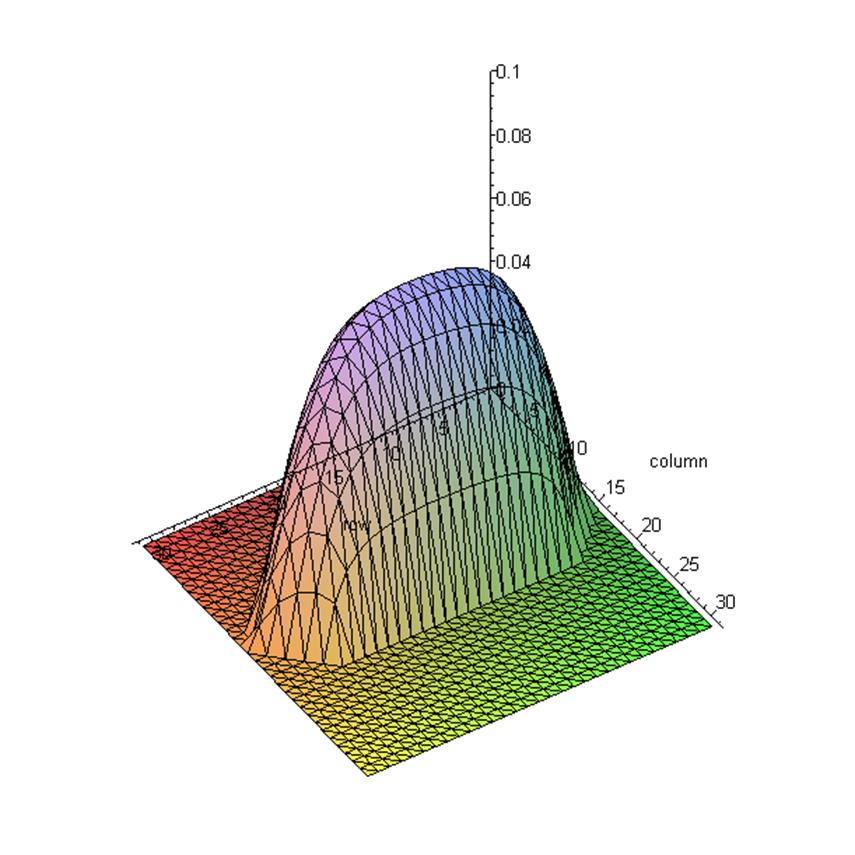
with(plots):matrixplot(Um,gridstyle=triangular,axes=normal,view=0..0.1);
Графическое представление решения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.