


Министерство общего и профессионального образования РФ
Хабаровский Государственный Технический Университет
Кафедра ВМ и П
Лабораторная работа № 4
По Мат. моделированию.
Тема: Надежность сложных технических систем
Выполнил: студент гр. ВМ-51
Лазебник В.Н.
Проверил: преподаватель
Корзова Л.Н.
1998 г.
Цель работы: Исследование функционирования сложных технических систем по показа-телям качества.
Задание:
1.По графу и структурной схеме определить тип технической системы, описать ее в терминах теории надежности и терминах теории массового обслуживания.
2.Определить интенсивности λik и νik или веса ребер графа системы для заданных значений L, r.
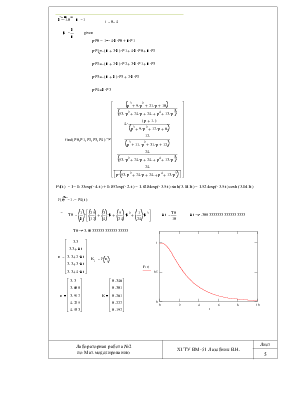
![]() 3. Построить по графу систему диф.
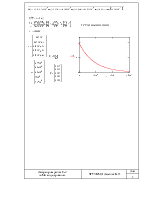
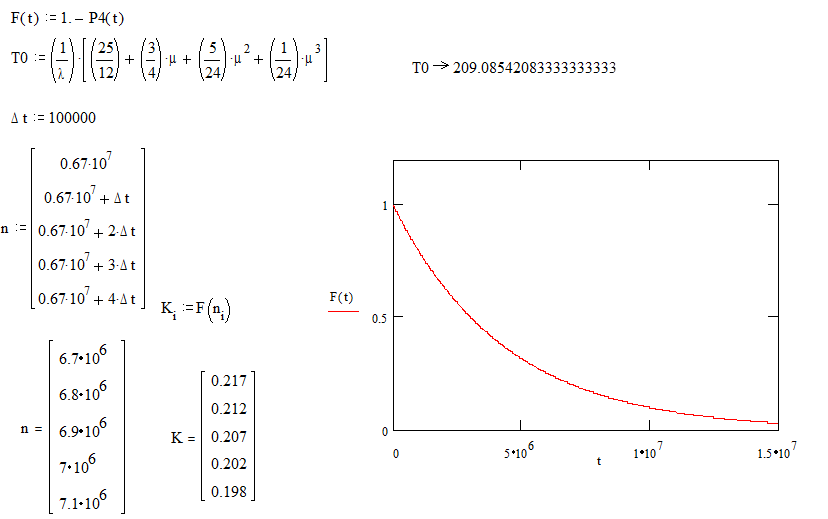
уравнений, решить ее. Использовать решение для построения функции надежности F(t). T0 определять по
формулам задания.
3. Построить по графу систему диф.
уравнений, решить ее. Использовать решение для построения функции надежности F(t). T0 определять по
формулам задания.
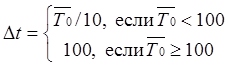 |
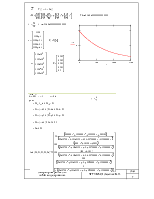
вычисления вести до тех пор, пока F(t)>0,2.
|
![]()
![]()
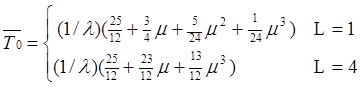 |
|
|
Кратность резервирования r=3
Количество наборов λ, ν: S=3
λ=1 λ=0,1 λ=0,01
ν=1 ν=1 ν=1
Рассматриваемая система есть система с частичным восстановлением, с постоянным резервированием.
Для L=1 система представляет собой одноканальную СМО с ожиданием, ограниченным входным потоком с интенсивностью λ, интенсивностью восстановления ν.
Для L=3 система представляет собой СМО с «бесконечным» числом каналов, ограниченным входным потоком с интенсивностью λ, взаимопомощью каналов и интенсивнос-тью восстановления ν.
Граф системы (L=1):
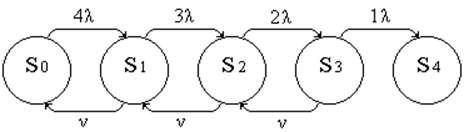 |
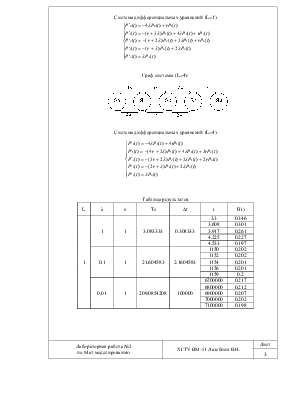
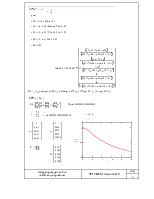
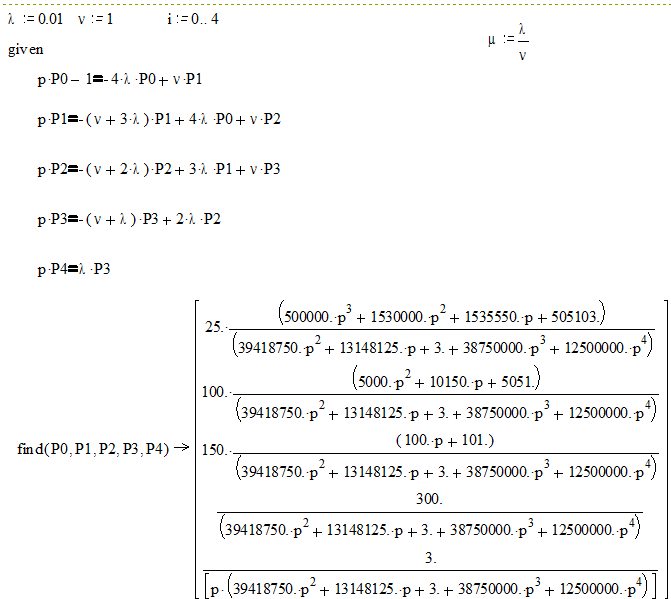
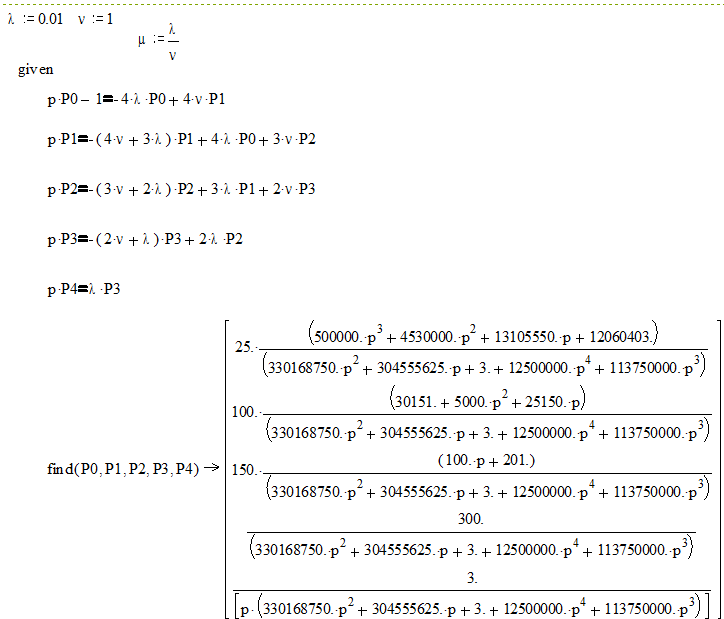
Система дифференциальных уравнений (L=1)
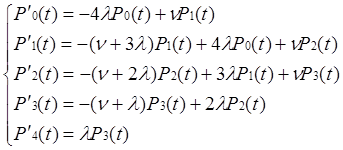 |
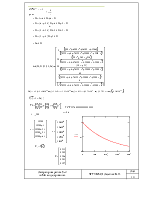
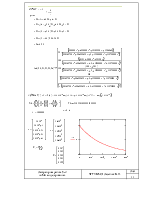
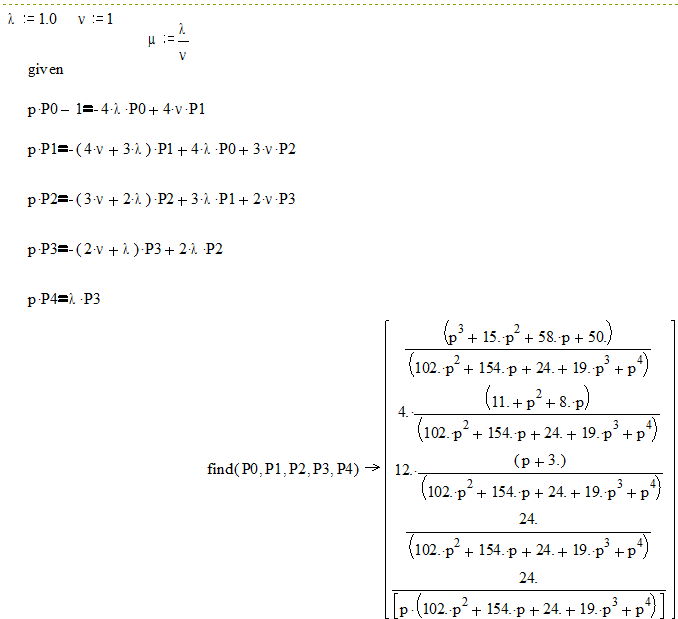
Граф системы (L=4):
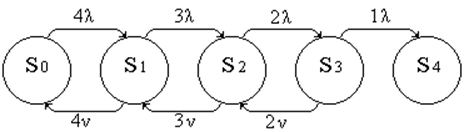 |
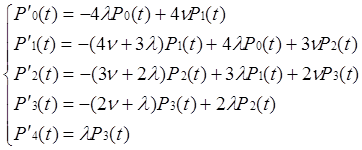 |
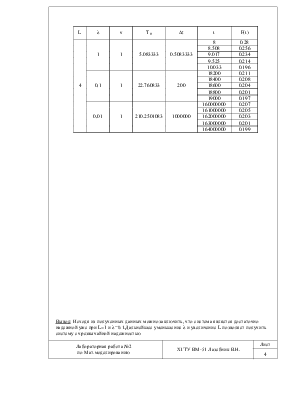
Таблица результатов
|
L |
λ |
ν |
T0 |
Δt |
t |
F(t) |
|
1 |
1 |
1 |
3.083333 |
0.308333 |
3.3 |
0.346 |
|
3.608 |
0.301 |
|||||
|
3.917 |
0.261 |
|||||
|
4.225 |
0.227 |
|||||
|
4.533 |
0.197 |
|||||
|
0,1 |
1 |
21.604583 |
2.1604583 |
1150 |
0.202 |
|
|
1152 |
0.202 |
|||||
|
1154 |
0.201 |
|||||
|
1156 |
0.201 |
|||||
|
1159 |
0.2 |
|||||
|
0,01 |
1 |
209.0854208 |
100000 |
6700000 |
0.217 |
|
|
6800000 |
0.212 |
|||||
|
6900000 |
0.207 |
|||||
|
7000000 |
0.202 |
|||||
|
7100000 |
0.198 |
|
L |
λ |
ν |
T0 |
Δt |
t |
F(t) |
|
4 |
1 |
1 |
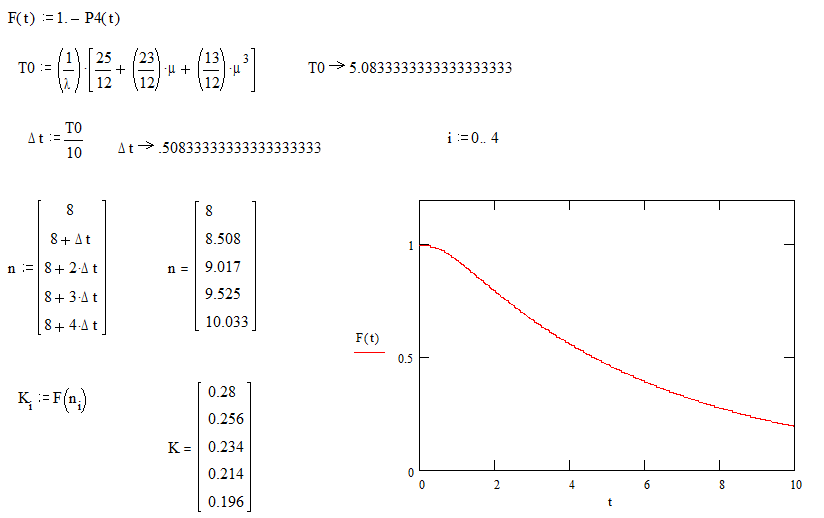
5.083333 |
0.5083333 |
8 |
0.28 |
|
8.508 |
0.256 |
|||||
|
9.017 |
0.234 |
|||||
|
9.525 |
0.214 |
|||||
|
10.033 |
0.196 |
|||||
|
0,1 |
1 |
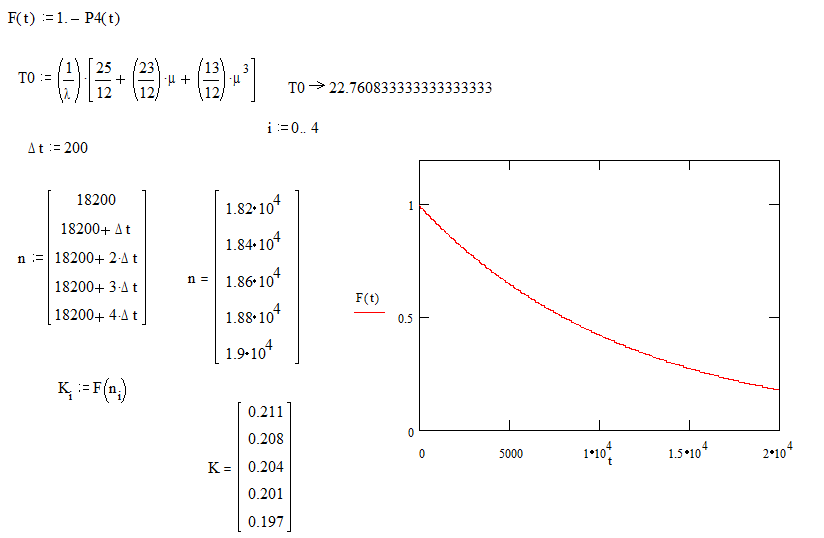
22.760833 |
200 |
18200 |
0.211 |
|
|
18400 |
0.208 |
|||||
|
18600 |
0.204 |
|||||
|
18800 |
0.201 |
|||||
|
19000 |
0.197 |
|||||
|
0,01 |
1 |
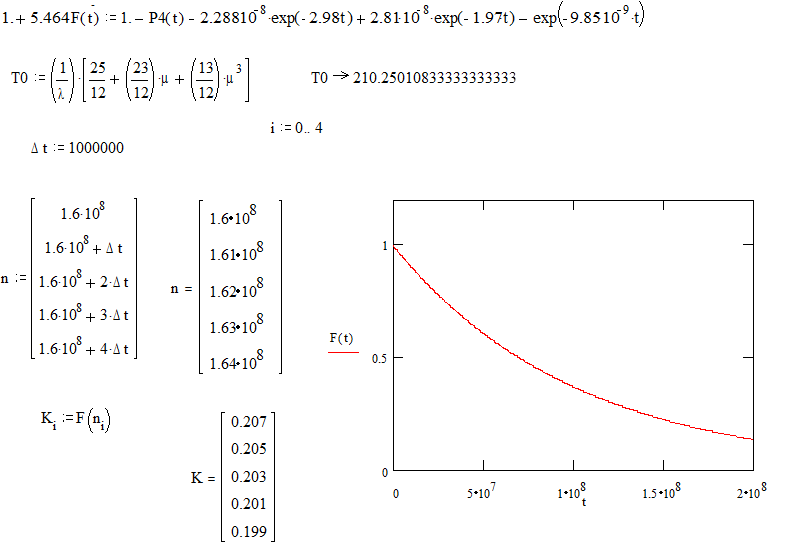
210.2501083 |
1000000 |
160000000 |
0.207 |
|
|
161000000 |
0.205 |
|||||
|
162000000 |
0.203 |
|||||
|
163000000 |
0.201 |
|||||
|
164000000 |
0.199 |
Вывод: Исходя из полученных данных можно заключить, что система является достаточно надежной уже при L=1 и λ=0.1.Дальнейшее уменьшение λ и увеличение L позволяет получить систему с чрезвычайной надежностью
 |
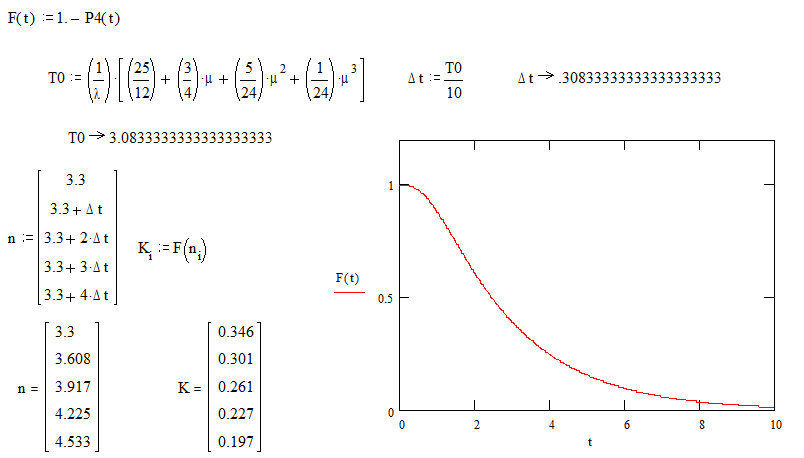 |
 |
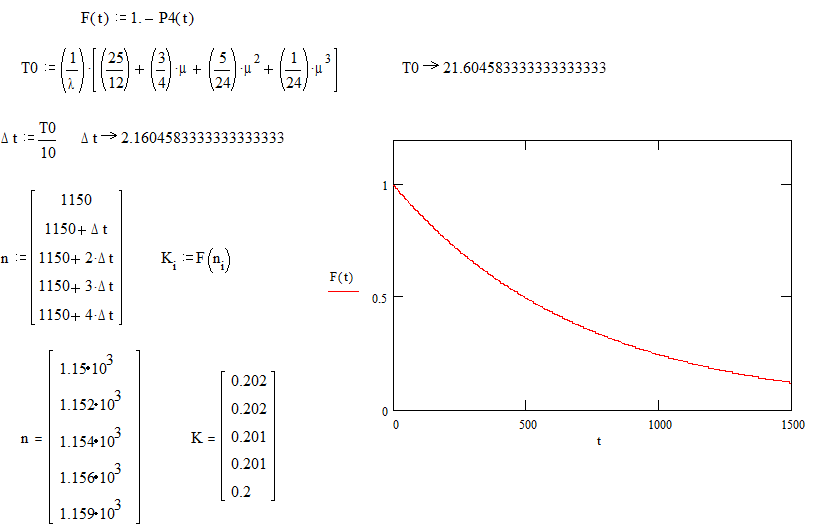 |
 |
 |
 |
 |
 |
 |
 |
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.