



Министерство общего и профессионального образования РФ
Хабаровский Государственный Технический Университет
Кафедра ВМ и П
Лабораторная работа № 3
По Мат. моделированию.
Тема: Моделирование многоканальной непростейшей СМО.
Выполнил: студент гр. ВМ-51
Лазебник В.Н.
Проверил: преподаватель
Корзова Л.Н.
1998 г.
Моделирование многоканальной непростейшей СМО.
Цель работы: Уметь моделировать сложные непростейшие СМО.
Задание: Смоделировать СМО с огрниченным временем пребывания требований в системе оценить ее по критериям эффективности.
Постановка задачи и алгоритмы псевдослучайных чисел:
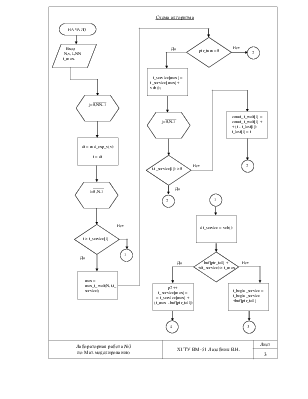
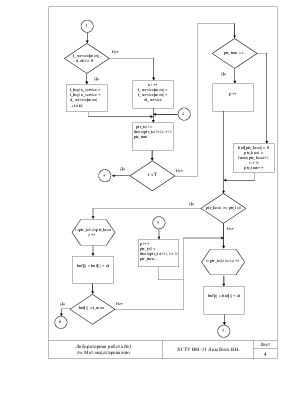
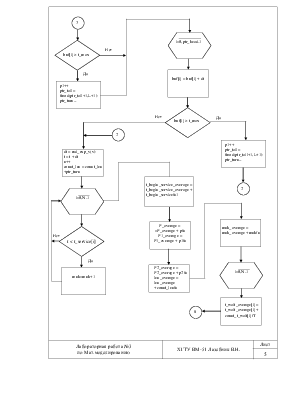
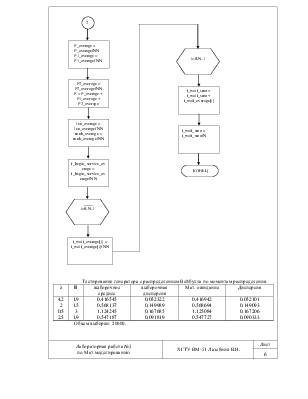
Необходимо методом Монте-Карло смоделировать работу непростейшей СМО с ограниченным временем пребывания требований в системе. Входной поток имеет распределение Пуассона, выходной поток имеет распределение Вейбулла. Необходимо найти следующие критерии эффективности:
- вероятность ухода требования из системы;
- вероятность отказа;
- вероятность того что требование будет обслужено;
- коэффициент занятости системы;
- коэффициент простоя системы
- средняя длина очереди;
- среднее число занятых каналов;
- среднее время начала обслуживания.
Для использования метода Монте-Карло необходим генератор псевдослучайных чисел с экспоненциальным законом распределения и которому, в свою очередь, необходим генератор с равномерным законом распределения на отрезке [0;1].
Алгоритм генератора с равномерным законом распределения:
zi=(a·zi-1+b)mod c; Ri=zi/c
Алгоритм генератора с экспоненциальным законом распределения:
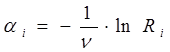
Алгоритм генератора с законом распределения Вейбулла:
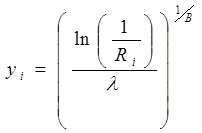
![]()
Ri – случайные числа, равномерно распределенные на [0;1].
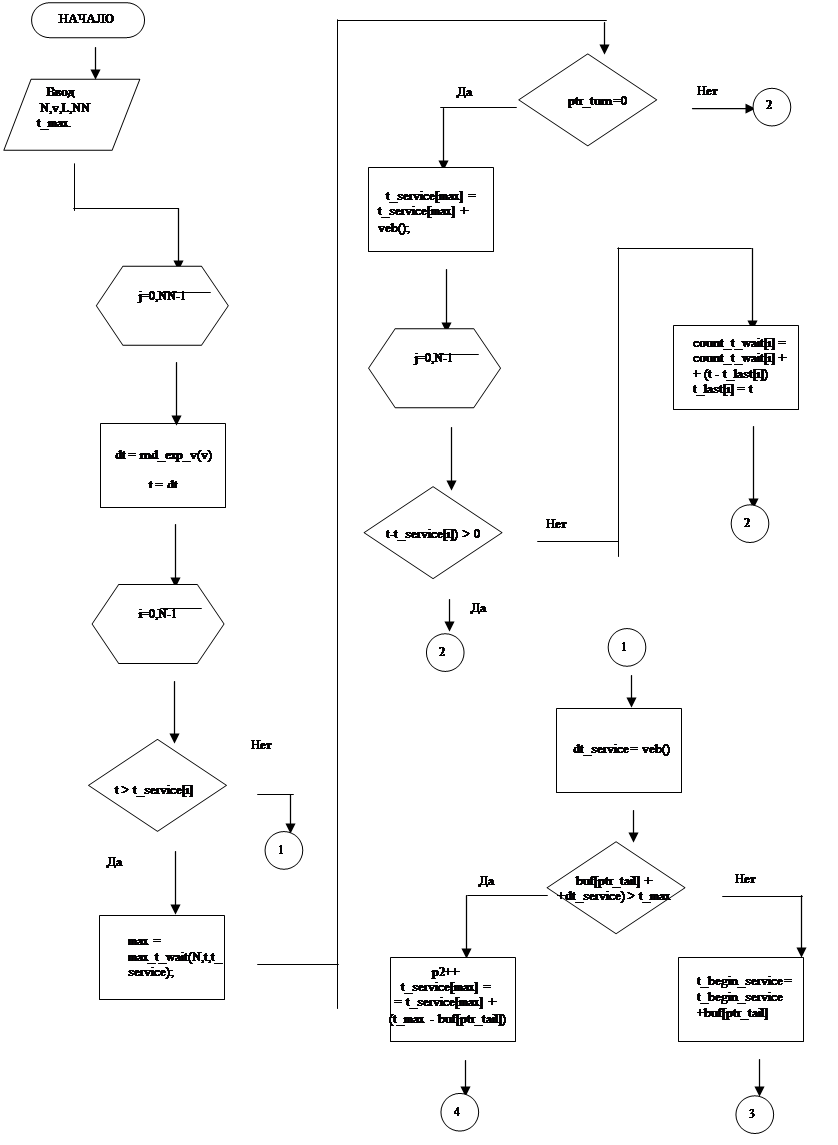
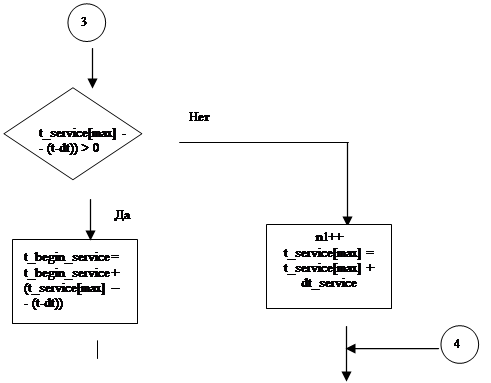 |
|||
 |
|||
![]()
 |
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.