Проектирование и расчет полосового усилителя с коэффициентом усиления: К0=20, страница 2

Исследуем ЛАЧХ активного ФНЧ.

АЧХ получим путем замены оператора Лапласа (p) на оператор jw и после взятия модуля от передаточной функции.

 

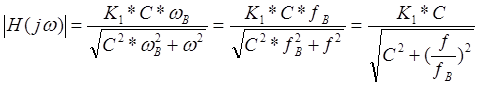После подстановки:

 

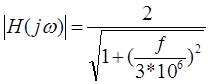Рассчитаем значения АЧХ и занесем их в таблицу 1:

¦, Гц	0	100	1000	10000	100000	1000000	2000000	3000000
|H(jw)|	2	2	2	1,99999	1,999	1,897	1,664	1,414
Log(¦)	-	2	3	4	5	6	6,301	6,477

¦, Гц	4000000	5000000	6000000	7000000	107	1,5*107	108
|H(jw)|	1,2	1,029	0,894	0,788	0,575	0,392	0,06
Log(¦)	6,602	6,699	6,778	6,845	7	7,176	8

 

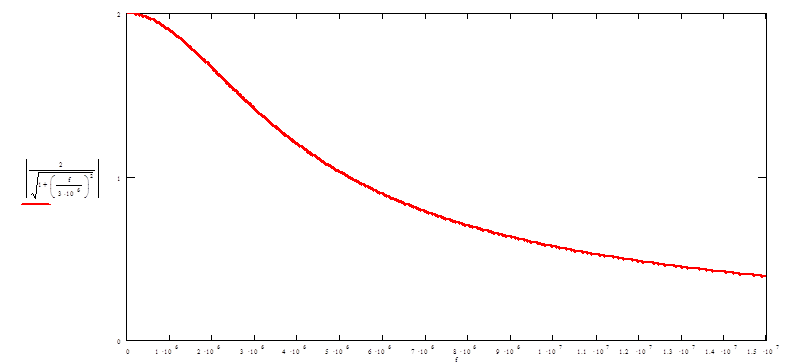Рис. 3. АЧХ активного ФНЧ.

 

Рис. 4. ЛАЧХ активного ФНЧ.

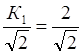Уровень передаточной функции равный                 соответствует верхней частоте среза ¦_В=3 МГц. Особенностью данного фильтра является то, что его полоса пропускания лежит в пределах от нулевой частоты до частоты среза.

3.4 Расчет логарифмической фазо-частотной характеристики (ЛАЧХ).

Исследуем ЛФЧХ активного ФНЧ.

Передаточную функцию фильтра можно представить в виде:

, где  - АЧХ, j(w) - ФЧХ.

j(w)=arg(H(jw)).

Для нахождения ФЧХ произведем преобразования передаточной функции, умножая знаменатель на комплексно-сопряженное значение:

 

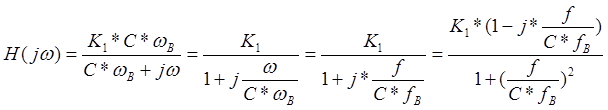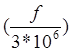Отсюда j(w)= - arctg

Рассчитаем значения ФЧХ и занесем в таблицу 2:

¦, Гц	0	10	102	103	104	105	106	2*106	3*106	4*106
j(w), рад	0	-3,33*10-6	-3,33*10-5	3,33*10-4	3,33*10-4	-0,0333	-0,322	-0,588	-0,785	-0,927
Log(¦)	-	1	2	3	4	5	6	6,301	6,477	6,602

¦, Гц	5*106	6*106	7*106	107	1,5*107	108
j(w), рад	-1,03	-1,107	-1,166	-1,279	-1,373	-1,541
Log(¦)	6,699	6,778	6,845	7	7,176	8

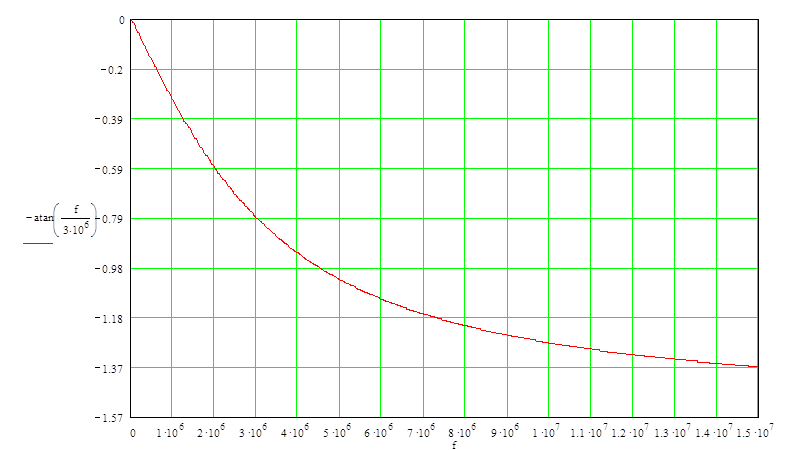
Рис. 5. ФЧХ активного ФНЧ.

 

Рис. 6. ЛФЧХ активного ФНЧ.

4. Проектирование и расчет ФВЧ.

4.1. Выбор и расчет принципиальной схемы ФВЧ.

Схема ФВЧ первого порядка приведена на рис. 7.

 

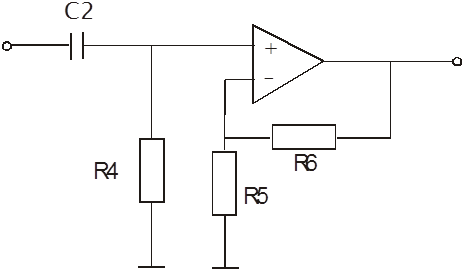Рис. 7. Схема фильтра верхних частот первого порядка.

Передаточная функция ФВЧ первого порядка в операторной форме:

 

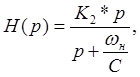где К₂ – коэффициент усиления звука,

С – коэффициент звена нижних частот (для фильтра                                                Баттерворта первого порядка С=1).

Найдем значения пассивных элементов схемы на рис. 7.

Значение емкости С₂ выбираем произвольно. Поскольку частота среза ¦_н примерно на два порядка меньше частоты среза ¦_в, то значение емкости С₂ выберем на два порядка больше, чем С1.

С₂=1 нФ.

Значения сопротивлений определяем из следующих соотношений:

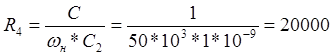                                                      Ом

Выбираем из ряда Е24 номинальное значение R₄=20 кОм.

                                                

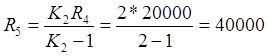
Ом  

Выбираем из ряда Е24 номинальное значение R₅=39 кОм.

                                                 Ом