Лекция № 3 Методы абстракции и элементы теории множеств, используемые при построении моделей данных
Как показано выше, одним из основных способов структуризации данных является использование абстракций для образования категорий данных (рис. 3.1):
Категория <тип объекта,тип свойства>
|
Идентификатор объекта |
Значение свойства |
Время |
Рисунок 3.1
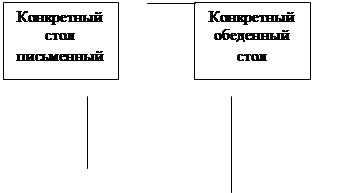
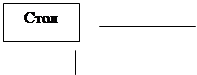
Для образования понятия тип объекта и тип свойства используется элементарная форма абстракции - ОБОБЩЕНИЕ. Введем ряд связанных с этим понятий. Под понятием ЗНАК будем подразумевать конкретное значение или конкретный экземпляр объекта. ТИП - класс подобных знаков. ОБОБЩЕНИЕ позволяет соотнести множество знаков или множество типов с одним общим типом. Обобщение знаков в типы в теории МД называется КЛАССИФИКАЦИЕЙ (рис. 3.2).
 |
 |
 |
|||
|
 |
|||
![]()
![]()
![]()
![]() ОБОБЩЕНИЕ
ОБОБЩЕНИЕ
|
Рисунок 3.2
Другой прием абстрагирования для построения структур данных-АГРЕГАЦИЯ. Под ней понимают абстракцию, посредством которой объект конструируется из других базовых объектов. Агрегация может использоваться как на уровне знаков, так и на уровне типов:
{кафедра ПО, международный отдел, PC AT386, 22.4.97}
или
{передающее подразделение, принимающее подразделение, объект, дата}.
Агрегация на уровне типов предполагает множество агрегаций на уровне знаков. В обработке данных эти абстракции применяются давно даже безотносительно к базам данных. Например, агрегация на уровне знаков порождает конкретные записи, агрегация на уровне типов данных, входящих в запись, определяет структуру, класс или тип записи.
В свою очередь обобщение для записей как для знаков дает понятие списка или файла.
АГРЕГАЦИЯ и ОБОБЩЕНИЕ применяются в МД взаимно-дополняющим образом и выражают структурные и классификационные аспекты типизации.
Математический аппарат, применяемый для описания структур в МД
включает:
¨ множества,
¨ расширенные множества,
¨ отношения и отображения.
КЛАССИЧЕСКОЕ МНОЖЕСТВО - совокупность правильно идентифицированных объектов, удовлетворяющих условию принадлежности. Например:
A={2,6,,12,16,14}; A1={конечное подмножество четных чисел};
A2={конечное множество чисел вида 2n, где n- натуральное}.
По аналогии с предыдущим можно сказать, что множество можно определить на уровне типов и на уровне знаков. ИНТЕНСИОНАЛ используется для определения совокупности множеств, обладающих заданными интенсионалом общими свойствами. Реализация (расширение) определяет конкретное множество путем явного перечисления значений его элементов.
 |
ИНТЕНСИОНАЛ Серия Номер Фамилия и паспорта паспорта инициалы
![]()
![]()
![]()
![]()
![]()
РЕАЛИЗАЦИЯ IV-ДВ 145897 Грачев П.И.
IV-ДВ 222333 Чуб С.П.
![]()
Рисунок 3.3
Еще одним примером интенсионала и реализации могут служить определение множества как совокупности 130 целых чисел, характеризующих число студентов присутствующих на лекции в начале каждой очередной ее минуты и множество
{24,24,24,25,25,25,25,25,26,26,....27,27,27}.
Приведенная здесь реализация не является классическим множеством, в котором запрещены идентичные объекты.
В классической теории множеств не предусматривается упорядоченность элементов множества, а дублирование не имеет смысла. Однако в МД упорядоченность данных существенно влияет на эффективность работы с ними, порядок данных часто используется также для отображения некоторых семантических свойств данных (например, хронологии).
Чайлдс Д. в 1974 году предложил термин "расширенное множество" или комплекс, определяющий базовое отношение i-ой принадлежности по аналогии с классическим множеством.
![]() Если
x есть i-ый элемент множества Y, то х находится в i-ой позиции множества Y:
Если
x есть i-ый элемент множества Y, то х находится в i-ой позиции множества Y:
x{ (i)Y.
Для любого i комплекс может иметь любое количество значений в позиции i. Позицию элемента в комплексе принято записывать с помощью верхнего индекса.
Пример:
{ b, c, d, a, b, m }
C точки зрения расширенных множеств, классическое множество это комплекс, все элементы которого расположены в одной позиции, а n- местный кортеж - комплекс, который имеет по одному элементу в каждой позиции от 1 до n.
Применение расширенных множеств обеспечивает достаточно большие возможности моделирования данных. В частности, расширенные множества позволяют представить дубликаты как размещение идентичных значений в различных позициях комплекса.
ОТНОШЕНИЯ
Бинарным отношением R, заданным на множествах A и B, является любое подмножество декартова произведения АхВ:
R [ AxB.
То есть множество R представляет собой совокупность пар кортежей
{ (a,b): a- A, b- B, R(a,b)=TRUE }, где R - условие принадлежности.
Пример: Отношение SL (учебная литература)
¦
¦Учебные
¦дисциплины
¦(Disc)
¦
Д6 ¦ *
¦
Д5 ¦ * *
¦
Д4 ¦ *
¦
Д3 ¦ * * *
¦
Д2 ¦ * * * *
¦
Д1 ¦ * * *
----+----------------------------------------------¦ К1 К2 К3 К4 К5 К6 К7 К8 Книги (Books)
R = { (К1,Д1),(К1,Д4),(К2,Д2), ... , (К8,Д2),(К8,Д6)}.
Вообще говоря, бинарное отношение задает отображение G между множествами А и В, возможно многозначное. В рассмотренном выше примере
G
К1 ----> {Д1,Д4} - образ элемента К1;
G
К2-----> (Д2,Д5) - образ элемента К2.
Отображение G для элемента a определяется как множество
G(a)={b: (a,b)- R}.
![]() Отображение
G множества А на множество В называется ФУНКЦИОНАЛЬНЫМ, если для каждого а множество
G(a) состоит не более чем из одного элемента.
Отображение
G множества А на множество В называется ФУНКЦИОНАЛЬНЫМ, если для каждого а множество
G(a) состоит не более чем из одного элемента.
Очевидно можно рассматривать обратное отображение F множества В на множество А. Например, для рассматриваемого примера:
F
Д6 ------> {K8},
Д3 ------> {K3,K5,K7}.
В общем случае F(a)={a: (a,b)- R}.
Каждое отношение как отображение можно характеризовать кардинальными числами Akmin, Akmax, Bkmin, Bkmax определяющими минимально возможное и максимально возможное число элементов в образе соответственно для обратного отображения F и прямого отображения G, задаваемых отношением R:
R(A(Аkmin,Akmax);B(Bkmin,Bkmax)).
Например, в примере с отношением SL (учебная литература) может быть установлено следующее ограничение, задаваемое кардинальными числами:
SL ( Disc(1,10);Books(1,3)).
Отношения третьего порядка R3 можно получить как бинарнoе отношение для множеств, одно из которых в свою очередь является отношением R2 второго порядка:
R3 R2*C
или
R3 C*R2.
Аналогично определяются отношения более высоких степеней.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.