Оценка нелинейных искажений роторной гармоники методом одного тона по коэффициенту искажения виброскорости или виброускорения

роскорости или в ограниченной полосе частот в сигнале по виброускорению. В последнем случае полоса фильтра в рабочем диапазоне скоростей вращения машины должна обеспечивать измерение виброускорения от первой до третьей роторных гармоник. Оценивают нелинейные искажения роторной гармоники методом одного тона по коэффициенту искажения виброскорости или виброускорения:

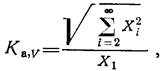
где Х1 — амплитуда первой роторной гармоники; Хi. — амплитуда i-й гармоники.

На практике амплитуды Хi определяют путем спектрального анализа.

Коэффициент искажения по виброперемещению из-за существенного ослабления высоких гармоник двукратным интегрированием сигнала, определяется крайне редко. В большинстве случаев форма низкочастотных вибраций по перемещению для турбома-шин близка к синусоидальной.

При наличии в машине нескольких одновременно вращающихся роторов или отдельных деталей возбуждаются вибрации с частотами пропорциональными скоростями вращения этих деталей. Если машина имеет общий привод, то вибрации имеют сложную форму с постоянным (без учета флуктуации частоты вращения) периодом колебаний. Математическая модель таких вибраций имеет вид

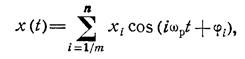
где Хi—амплитуда 1-й частоты; Wр—частота вращения ротора (m=1); Фi—начальная фаза 1-й частоты; n—число независимых частот вибраций; m>0.

Если амплитуда Xi постоянна, то такие вибрации удовлетворяют требованиям периодичности колебаний, т. е.

где i=1, 2, 3....

В действительности при постоянной скорости вращения привода наблюдаются флуктуации амплитуд Xi и частот кор. Поэтому их описание выражением (1.5) является приблизительным и выявлять нелинейные преобразования вибросигналов в таких машинах становится довольно трудной задачей, особенно в тех случаях, когда имеются кратные передаточные отношения в машине. Такие вибрации обычно имеют дискретный спектр.

У многороторных машин, роторы которых связаны не механически, а газодинамически (например, многороторные газотурбинные двигатели или несколько двигателей на одном объекте) вибрации имеют достаточно сложную форму. Такие вибрации на отдельных режимах работы машины могут удовлетворять требованию периодичности колебаний (1.6), а могут и не удовлетворять этому требованию, т. е. быть непериодическими, хотя спектр может быть дискретным. Нарушение требования (1.6) имеет место только тогда, когда виброcигнал содержит две или более дискретных составляющих с иррациональным отношением частот и как следствие, основной период становится равным бесконечности [2]. Эти процессы называют почти периодическими и описываются они в функции времени выражением (1.5). Форма вибросигнала таких процессов зависит от их частотного состава, отношения частот и. амплитуд, а также начальных фазовых сдвигов относительно основной частоты. Среднее квадратичное значение вибросигналов, описываемых выражением (1.5), определяется как

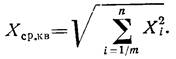
Аналитическое выражение для среднего значения можно получить только для постоянных отношений амплитуд и начальных фазовых (сдвигов. В действительности таких вибраций практически не существует. Поэтому математическая модель многокомпонентной вибрации с изменяющимися амплитудами для случая их аддитивной смеси имеет вид

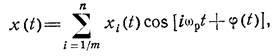
а среднее значение

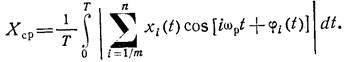
Из последнего выражения видно, что при постоянных значениях i и Wр среднее значение Хср зависит от амплитуды Хi(t) и фазы

Фi(t.

Характерным является случай сложения вибросигналов от двух роторов, частоты которых могут взаимно перекрываться. Тогда возможно равенство частот, незначительное отличие частот друг от друга и значительное отличие частот. В случае значительной разницы частот f1/f2@10 сдвиг фаз не оказывает существенного влияния на Хср и форму сигнала. Когда же частоты незначительно • отличаются друг от друга, то Хср и форма сигнала зависят от сдвига фаз и отношения амплитуд.

Пусть X1(t =Х1mSIN (WT+Ф) и Х2 (t) =Х2m SIN (а +@) t, где Х1m и Х2m—максимальные амплитуды на частотах W и W+@ соответ-