Определение теплоёмкости воздуха. Освоение методики калориметрического эксперимента на примере определения изобарной теплоёмкости воздуха, страница 2

Пусть при бесконечно малом изменении состояния тела количество теплоты dQ вызывает изменение температуры тела dT, тогда теплоёмкость тела в данном процессе выразится отношением:

или

Единицей теплоёмкости является Дж/К.

Теплоёмкость С зависит от внешних условий или характера процесса, при котором происходит отвод или подвод теплоты. Так, например, теплоёмкость газов в случае подвода теплоты при постоянном объеме  отличается от удельной теплоёмкости газов при постоянном давлении .

Удельная теплоёмкость есть отношение теплоёмкости к массе вещества.

.

Если С выражается в Дж/К, m – в кг, то с – в Дж/(кг·К).

Объёмная теплоёмкость [Дж/(м·К)]

, где  и  – плотность и объём газа при нормальных физических условиях, кг/м; м.

Молярная теплоёмкость [Дж/(м·К)]

, где n – количество рабочего вещества, моль.

3.  Формула Майера.

4.  Формула для определения количества тепла при постоянной и переменной теплоёмкостях.

Пользуясь истинной удельной теплоёмкостью, требуёмое количество теплоты для  нагрева m вещества от температуры  до ºС определим из выражения:

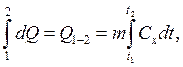
где 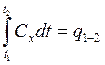 – требуемое количество теплоты.

Здесь интеграл берётся по пути процесса от 1 до 2 (от начального состояния до заданного конечного), так как изменение температуры тела зависит от характера процесса, а с этим связанно изменение теплоёмкости тела . Удельное количество теплоты  является, таким образом, функцией процесса и не является поэтому функцией состояния системы, изменения которой зависит только от начального и конечного состояний.

Теплоёмкость газа не постоянна. Для идеального газа она является функцией температуры. Теплоёмкость зависит от температуры, а также от давления и объёма. При низких давлениях и высоких температурах теплоёмкость газа считают приближенно зависящей от температуры.

В общем случае истинная теплоёмкость для температуры t с достаточной степенью точности выражается для большинства газов уравнением второй степени (нелинейным)

, где a, b, e – постоянные, определяемые для различных газов и видов теплоёмкости на основании экспериментальных и теоретических данных.

Количество теплоты в изохорном термодинамическом процессе:

и

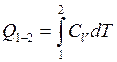
а при

где  – удельная теплоёмкость тела при постоянном объёме.

Количество теплоты изобарном термодинамическом процессе:

и

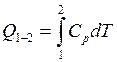
а при

где  – удельная теплоёмкость тела при постоянном давлении.

Количество теплоты в изотермическом термодинамическом процессе:

.

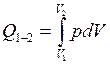5.  Физический смысл внутренней энергии и энтальпии газа. Формулы для их вычисления.

Внутреннюю энергию рассматривают с молекулярной точки зрения как сумму кинетической и потенциальной энергий, обусловленных хаотическим движением и взаимодействием молекул газа. Другие виды энергии не учитываются, так как при рассматриваемых в технической термодинамике температурах их влиянием на изменение состояния можно пренебречь.

Для реальных газов внутренняя энергия является функцией как температуры , так и плотности газа :

.

Внутреннюю энергию можно найти из первого закона термодинамики:

,

Для изохорного процесса.

Для изобарного .

Для изотермического

Для адиабатного .

Параметром состояния газа наряду с внутренней энергией является удельная энтропия:

она определяется исключительно функциями состояния ().

Энтальпия имеет особо важное значение для техники в случае непрерывного потока рабочего тела. С ее помощью значительно упрощаются рассмотрения процессов и их расчеты.

Величина i выражается в Дж/кг, если слагаемые u и pv – в Дж/кг.

Энтальпия представляет энергию, связанную с данным состоянием тела, т. е. является функцией состояния, поскольку u и pv – функции состояния.

В процессе с постоянным давлением :

т.е. изменение удельной энтальпии равно количеству теплоты, подведенной к телу при .

Из выражения находим:

или

Энтальпия  – экстенсивная (аддитивная) величина. Удельная энтальпия  обладает интенсивными свойствами.

Удельную теплоёмкость при постоянном давлении  можно определить следующим образом:

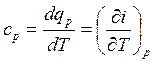
но

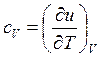
Сравнивая последние два выражения, видим, что при постоянном давлении удельная энтальпия обладает свойствами, аналогичные тем, которые имеет внутренняя энергия при постоянном объёме.

Из определения удельной энтальпии:

Поскольку внутренняя энергия  является лишь функцией температуры, то  также зависит только от температуры. Отсюда для идеального газа:

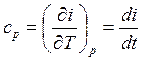
а при  находим:

и для любого изменения от состояния 1 до состояния 2

6.  Сущность калориметрического метода определения теплоёмкости газа.

Опытное определение изобарной теплоемкости газа сводиться к нагреву его в проточном калориметре и измерению необходимых величин (количества тепла , объёмного расхода  и повышения температуры ). Полагая, что все тепло от электронагревателя идёт в установившемся процессе на изобарный нагрев воздуха (тепловые потери отсутствуют), теплоёмкость можно найти по формуле, :

Вывод

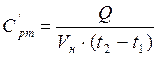
Я изучил первый закон термодинамики и все виды теплоёмкостей газов. Освоил методику калориметрического эксперимента на примере определения изобарной объёмной теплоёмкости воздуха, которая равна 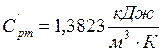, величина расхождения между экспериментально определенной теплоёмкостью  и табличным значением  равна %, это обусловлено погрешностью измерений и нагрева воздуха от электронасоса.