Р = Ме расч· ί1/ r1в= 103·3.56/0.06 = 6000 (124)
Радиусы кривизны в полюсе зацепления, м
Р1 = r1·sinα = 29·sin 20 = 29·0.342 = 9.9 мм = 0.0099 м (125)
Р2 = r2·sinα = 60·sin 20 = 60·0.342 = 20.5 мм = 0.0205 м (126)
Окончательно для первой передачи имеем, МПа
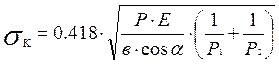 =
= 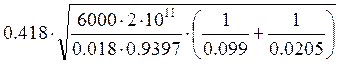 = 639
(127)
= 639
(127)
σк-контактные напряжения в полюсе зацепления шестерен;
Р- нормальное давление между зубьями в полюсе зацепления;
Е- модуль упругости первого рода;
p1 , p2 радиусы кривизны зубьев в полюсе зацепления соответственно ведущей и ведомой шестерен.
в- рабочая длина контакта.
Расчёт показал, что контактные напряжения в зубьях шестерен первой передачи находятся в допустимых пределах для цианируемых зубьев.
Для косозубого зацепления расчет производим пары постоянного зацепления первичного и промежуточного валов.
Исходные данные:
в = 18мм = 0.018 м;
α =20˚;
β = 24˚
С =
88.6 мм = 0.0886 м
Расчетный момент, Нм
Мерасч = 0.5· Меmax = 0.5·206 = 103. (128)
Радиусы начальных окружностей, м
r1 =С/1+ ί'к = 88.6/1+1.7 = 33 мм = 0.033 м (129)
r2 = r1· ί'к = 33 · 1.7 = 56 мм = 0.056 м (130)
Окружное усилие на шестерне первичного вала, Н
Р = Ме расч / r1= 103/0.033 = 3121 (131)
Радиусы кривизны поверхностей зубьев в полюсе зацепления, м
Р'1 = r1·sinα/cos![]() β = 33·sin 20/cos
β = 33·sin 20/cos![]() 24 =
33·0.342/0.8345 = 15 мм (132)
24 =
33·0.342/0.8345 = 15 мм (132)
Р'2 = r2·sinα /cos![]() β = 56·sin 20/cos
β = 56·sin 20/cos![]() 24 =
56.342/0.8345 = 23 мм (133)
24 =
56.342/0.8345 = 23 мм (133)
Окончательно для зацепления имеем, МПа
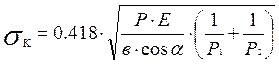 =
= 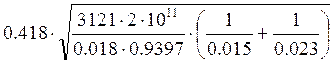 =
791 (134)
=
791 (134)
Расчёт показал, что контактные напряжения в зубьях шестерен постоянного зацепления находятся в допустимых пределах практически для обоих видов упрочнения поверхности зубьев.
2.3.5 Расчет промежуточного вала на прочность
2.3.5.1 Определение сил и реакций в подшипниках
Силы действующие на промежуточный вал:
Окружная
сила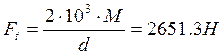 , (135)
, (135)
Радиальная
сила 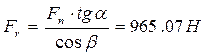 , (136)
, (136)
Определим реакции связи:
Рассмотрим плоскость YOZ:
![]() ,
(137)
,
(137)
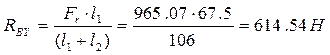 . (138)
. (138)
![]() ,
(139)
,
(139)
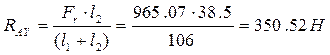 . (140)
. (140)
Проверка:
![]() ,
, ![]()
Рассмотрим плоскость ХOZ:
![]() ,
(141)
,
(141)
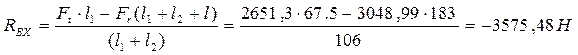 .
.
![]() , (142)
, (142)
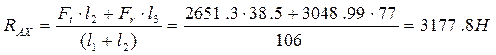 .
.
Проверка:
![]() ,
, ![]()
Построим эпюры моментов:
Рассмотрим плоскость YOZ:
1. ![]() ,
, ![]()
![]() ,
, ![]()
2. ![]() ,
, ![]()
![]()
![]() ,
,
3. ![]()
Рассмотрим плоскость ХOZ:
1. ![]() ,
, ![]()
![]() ,
, ![]()
2. ![]() ,
, ![]()
![]()
![]() ,
,
3. ![]()
Момент
крутящий ![]()
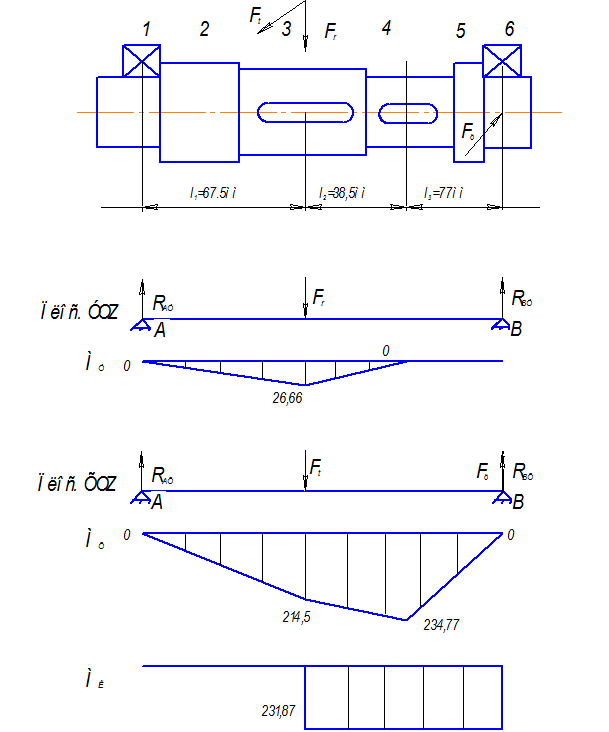
Рис. 6- Эпюры.
2.3.6 Расчет промежуточного вала на выносливость
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.