Расчет привода при выборе двигателя АИР100S4

Число N_HG циклов, соответствующее перелому кривой усталости, определяют по средней твердости поверхности зубьев:

,

Ресурс N_k передачи в числах циклов перемены напряжений при частоте вращения n и времени работы L:

,

.

Коэффициент долговечности Z_N учитывает влияние ресурса

,

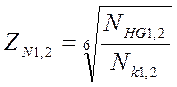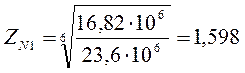
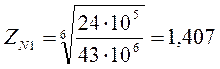
Коэффициент Z_R, учитывающий влияние шероховатости сопряженных поверхностей зубьев, принимают для зубчатого колес пары с более грубой поверхностью зависимости от параметра шероховатости (Z_R=1).

Коэффициент Z_υ учитывает влияние окружной скорости. При НB≤350HB

,

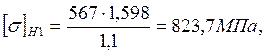
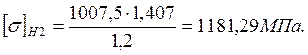
Значение коэффициента К_Hv внутренней динамической нагрузки для прямозубых конический колес выбирают в зависимости от степени точности и твердости поверхности зубьев колеса (К_Hv=1,15).

Коэффициент К_Hβ учитывает неравномерность распределения нагрузки по длине контактных линий. Для конических колес с прямыми зубьями

где К⁰_Hβ – коэффициент, определяемый в зависимости от отношения ψ_bd=b/d_e1, твердости зубчатых колес и расположения передачи относительно опор. Так как ширина зубчатого венца b и диаметр шестерни d_e1еще не определены, значение коэффициента ψ_bd вычисляют ориентировочно:

К⁰_Hβ=1,5

Находим значение диаметра внешней делительной окружности шестерни:

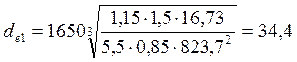→ 36 мм

Находим значение диаметра внешней делительной окружности колеса:

.

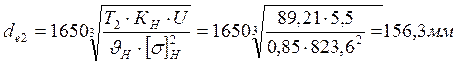Округляем полученное значение по нормальному ряду до 160мм.

Уточняем значение диаметра внешней делительной окружности шестерни:

.

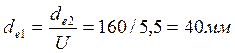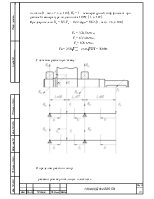
2.3 Конусное расстояние и ширина зубчатого венца

Угол делительного конуса шестерни

Внешнее конусное расстояние

Ширина зубчатого венца

b= 0,285R_e=0,285∙82,46=23,5→ 25 мм

2.4 Модуль передачи

Внешний торцовый модуль передачи для конических колес с прямыми зубьями

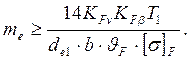
Значение коэффициента К_Fv внутренней динамической нагрузки для прямозубых колес выбирают в зависимости от точности (К_Fv=1,30).

Коэффициент К_Fβ учитывает неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца. Для конических передач с прямыми зубьями

К_Fβ= К΄_Fβ=0,18+0,82 К⁰_Hβ=0,18+0,82∙1,5=1,41

Вместо [σ]_F в расчетную формулу подставляют меньшее из значений [σ]_F1 и [σ]_F2. Допускаемые напряжения изгиба зубьев шестерни и колеса определяют по общей зависимости, учитывая влияние на сопротивление усталости при изгибе долговечности, шероховатости поверхности выкружки и реверса нагрузки:

Предел выносливости σ_Flim вычисляют по эмпирическим формулам:

 МПа,

 МПа.

Минимальное значение коэффициента запаса прочности для улучшенных зубчатых колес S_F=1,7.

Коэффициент долговечности Y_N учитывает влияние ресурса при условии 1≤Y_N ≤Y_Nmax:

где Y_Nmax1=4 и q₁=6 для улучшенных зубчатых колес,  Y_Nmax2=2,5 и q₂=9 для закаленных зубчатых колес. Число циклов, соответствующее кривой усталости, N_FG=4·10⁶.

Назначенный ресурс N_k вычисляют так же, как и при расчетах по  контактным напряжениям.

N_k1= 23,6∙10⁷

N_k2=43∙10⁶

В соответствии с кривой усталости напряжения σ_F не могут иметь значений меньших σ_Flim. Поэтому при N_k>N_FG принимают N_k=N_FG.Следовательно Y_N=1.

Коэффициент Y_R, учитывающий влияние шероховатости переходной поверхности между зубьями принимают равным единице.

Коэффициент Y_A  учитывает влияние двухсторонней нагрузки. При одностороннем приложении нагрузки Y_A =1.

Вычисляем значение модуля передачи:

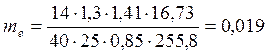
Округляем значение модуля до 1.

2.5 Числа зубьев

Определим число зубьев шестерни (z₁) и колеса (z₂):

.

2.6 Фактическое передаточное число

Значение фактического передаточного числа не должно отличатся от  заданного не более чем на 3% для конических редукторов.

2.7 Окончательные значения размеров колес

Вычисляем углы делительных конусов шестерни и колеса:

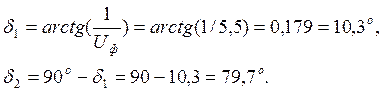
Вычисляем делительные диаметры колес:

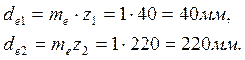
Вычисляем внешние диаметры колес:

,

.

Где х_е1  – коэффициент смещения для шестерни,

х_е1=0,43,

х_{е2 –} коэффициент смещения инструмента для колеса,

х_е2=- 0,43.

2.8 Размеры заготовки колес

Для конических шестерни и колеса вычисляют размеры заготовки:

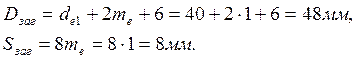
Полученные расчетом значения размеров заготовки сравнивают с предельными размерами.

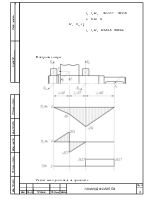
2.9 Силы в зацеплении

Окружная сила на среднем диаметре шестерни:

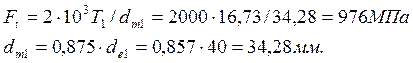
Осевая сила на шестерне:

МПа

где α=20˚.

Радиальная сила на шестерне:

МПа

Осевая сила на колесе:

МПа

Радиальная сила на колесе:

МПа

2.10 Проверка зубьев колес по контактным напряжениям.

Расчетное контактное напряжение

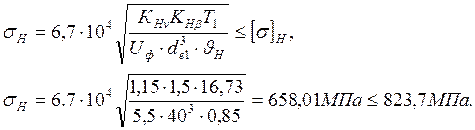
2.11 Проверка зубьев колес по напряжениям изгиба

Напряжение изгиба в зубьях колеса:

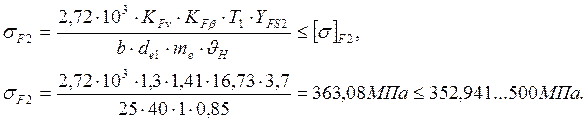
Значение коэффициента Y_FS2, учитывающего форму зуба и концентрацию напряжений, принимают в зависимости от приведенного