Резьбовые соединения. Основные параметры резьбы. Расчет болтов, подверженных переменной нагрузкой. Расчет резьбы на прочность

период затяжки болт испытывает и растяжение и кручение. Напряжение растяжения от F_зат, возникающее от затяжки болта,

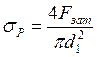
Напряжение кручения от момента в резьбе

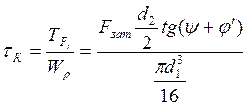, где  - угол подъема винтовой линии;  - угол трения.

Эквивалентное напряжение в болте по гипотенузе формоизменения

.

Отношение напряжений

.

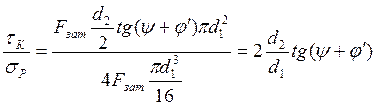Принимая для метрической резьбы с крупным шагом ,  и , получим 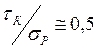. Тогда . Т.е., расчет болта на совместное действие растяжения и кручения можно заменить расчетом на растяжение, принимая для расчета не силу затяжки , а расчетную , увеличенную с учетом кручения:

для метрических резьб , для трапецеидальных

для упорных и прямоугольных

С учетом изложенного расчетная формула для определения прочности болта примет вид с учетом крутящего момента и затяжки

 или,

Здесь F – внешняя нагрузка, приходящаяся на 1 болт.

При таком способе загрузки болта допускаемое напряжение определяется

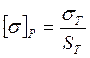, где S – требуемый коэффициент запаса прочности, который при неконтролируемой затяжки принимают по таблице в зависимости от материала, характера нагрузки и диаметра резьбы.

Таблица 16.1

Сталь	Постоянная нагрузка			Переменная нагрузка
	от 6 до 16	от 16 до 30	от 30 до 60	от 6 до 16	от 16 до 30	от 30 до 60
Углеродистая Легированная	5-4 6,6-5	4-2,5 5-3,3	2,5-1,6 3,3	10-6,5 7,5-5	6,5 5	6,5-5 5-4

Для силовых соединений не допускаются болты диаметров меньше 8 мм, т. к. болты малых диаметров легко разрушить при затяжке.

При контролируемой затяжке (специальными динамометрическими клячами)  величина  не зависит от . В этом случае

-  для углеродных сталей ;

-  для легированных сталей

Большие значения коэффициента запаса прочности принимают при невысокой точности определения действующих нагрузок или для конструкций повышенной ответственности.

2. Соединение, нагруженное поперечными силами, сдвигающими детали в стыке

1. Болты поставлены с зазором (рисунок 16.11).

 

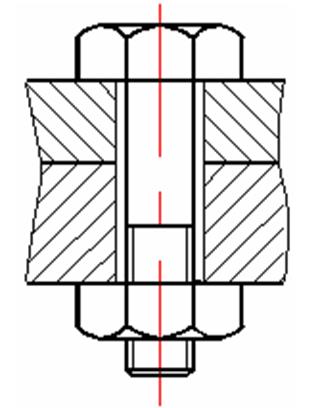
Рисунок 16.11 – Болты с зазором

В случае если , болт выберет зазор и будет работать на изгиб и быстро не разрушится. Изобразим осевую нагрузку  дадим коэффициент трения , тогда , где  – количество плоскостей среза; отсюда

_.

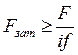Из условия растяжения         .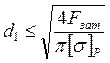

Вместо  подставили  и получили

.

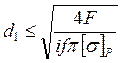Болт, поставленный в отверстие с зазором работает на растяжение (при условии )

Р

2. Болты поставлены без зазора (рисунок 16.12).

 

d

dH

F

F

		Р

 

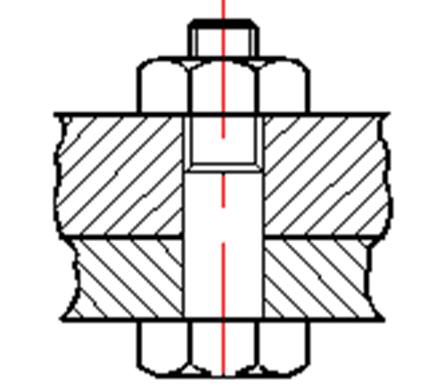
Рисунок 16.12 – Болты поставлены без зазора

Отверстие калибруется, а болт ставится с допуском, обеспечивающим беззазорную посадку.

Болты, естественно, проверяются на срез. Всю нагрузку будет принимать диаметр с натягом .

,

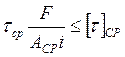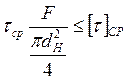, где  - для стальных болтов - ;  – при соединении 3-х деталей и           – при соединении 2-х деталей.

16.6 Расчеты группы болтов

1. Внешняя сила проходит через центр тяжести соединения

Группа болтов нагружена усилиями, равнодействующая которых перпендикулярна к плоскости стыка, проходит через центр его тяжести. Болты в этом случае нагружены равномерно (рисунок 16.13).

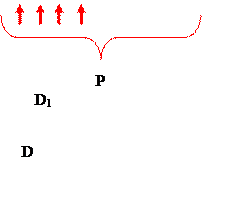
Рисунок 16.13

Внешняя нагрузка на все болты

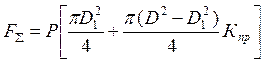, где p – давление, К_пр – коэффициент, учитывающий материал и форму прокладок (для мягких прокладок – войлок, резина К_пр=1,5…2,8; для металлических плоских К_пр=3,2…5,3).

Внешняя нагрузка на один болт:

, где z – число болтов.

Расчетная нагрузка на болт  

Используя выведенную ранее зависимость для , имеем

2. Нагрузка соединения сдвигает детали в стыке

1. Болты с зазором и нагружены крутящим моментом в области стыка.

Основное условие не раскрытия стыка: момент сил трения больше внешнего момента, т. е. T_тр>T

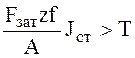, откуда  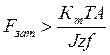                                     , где F_зат – усилие затяжки болта, Z – число болтов, f – коэффициент трения, S – площадь стыка, – статический полярный момент инерции стыка относительно главных центральных осей, Т – действующий крутящий момент.

Для кольцевого стыка пользуются приближенной формулой с учетом того, что F_тр в стыке отнесена к осям винтов:

.

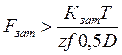Опираясь на условие реактивных моментов для стыка произвольной симметричной формы, т. е. внешний момент, уравновешенный моментами трения в болтах:

Отсюда

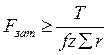
Для нашего конкретного стыка будем иметь:

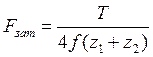
2. Болты без зазора для кольцевого стыка рассчитываются на срез по усилию:

.

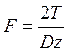Для стыка произвольной симметричной формы тоже на срез по усилию .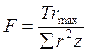

3. Нагрузка соединения раскрывает стык деталей

Соединение нагружено изгибающим моментом, открывающими и срезывающими усилиями.

Раскладываем R на составляющие R_x и R_y и приведем составляющие силу R (R_x и R_y) к центру тяжести стыка (т. о.). Появятся два момента R_xH и , направленные в разные стороны. Предположим, что , тогда .

Итак, на соединение действуют силы R_x, R_y и момент М.

Пусть на болты действует  и , тогда на стык будет действовать соответственно  и

Напряжение в стыке алгебраически складывается из напряжений от отрывающей силы (разгружающей стык) :

.

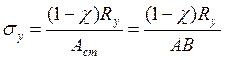Напряжений от момента М:

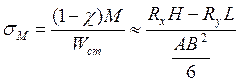
Напряжений затяжки стыка , определяемых из условия не раскрытия стыка

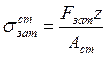, где z – число болтов, F_зат – усилие затяжки 1 болта, А_ст=АВ – площадь стыка.

Как – уже было отмечено, сила  уменьшает напряжение в стыке, а момент , стремясь повернуть кронштейн по часовой стрелке