Определение коэффициента взаимной индукции двух соленоидов, страница 2

где:  – магнитная проницаемость среды, заполняющей соленоид (в нашем случае это воздух - =1);  – магнитная постоянная (=4); N₁ – число витков в соленоиде;  – длина соленоида.

Определим теперь потокосцепление, то есть магнитный поток, проходящий через площадь всех витков второго контура (число витков равно N₂, площадь витка S₂)

Представляя выражение для В (формула 2) получаем:

                                                                       (3)

Сравнивая формулы (1) и (3) получаем для коэффициента взаимной индукции соосных соленоидов:

                                                               (4)

Если соленоиды не сосны, а их оси составляют друг с другом угол , то  коэффициент взаимной индукции уменьшается и будет:

                                                              (5)

В лабораторной работе используется переменный электрический ток, который идёт по виткам длинного соленоида. В результате, внутри соленоида возникает переменное магнитное поле, которое, в соответствии с законом электромагнитной индукции Фарадея вызывает появление переменной ЭДС индукции () на зажимах второго контура:

Подставляя соотношение (1) имеем:

                                                                              (6)

Сила тока в первом контуре изменяется по закону:

где  – амплитуда тока (А);  – частота переменного тока (Гц). Подставив выражение для силы тока  в (6) получим:

Из последней формулы следует, что амплитуда напряжения на зажимах второго контура будет равно:

  

Из последней формулы ясно, что коэффициент взаимной индукции может быть определён, если измерены :

                                                                (7)

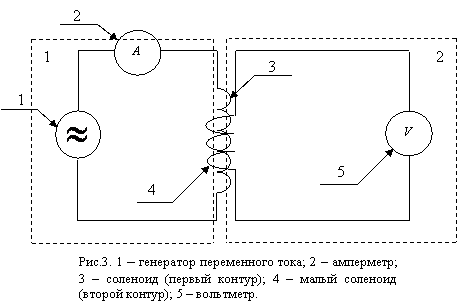Принципиальная схема установки

Описание лабораторной установки

Электрическая схема лабораторной установки (рис.3) включает генератор переменного тока, первый контур, представленный длинным соленоидом и второй контур (катушка малого диаметра), размещённый внутри длинного соленоида. Катушка может вращаться вокруг вертикальной оси. Угол поворота между осями длинного соленоида и катушки может быть определен по лимбу, размещённому на длинном соленоиде. В установке имеется вольтметр для измерения напряжения на зажимах второго контура.