Расчет реактора синтеза метанола

стехиометрические числа стадий в соответствующем маршруте. Нулевое значение стехиометрического числа указывает на неучастие  данной стадии в данном маршруте.

В основу схемы заложен окислительно-восстановительный механизм. Химическое превращение попадает в ранг многомаршрутных реакций. Теория многомаршрутных реакций позволяет получить кинетическое уравнение химического превращения, если один из маршрутов находится в состоянии равновесия. В нашем случае лимитирующая стадия адсорбции водорода является общей для  маршрутов, следовательно, равновесного маршрута нет. В рамках теории многомаршрутной реакции:

Стадии 1), 2), 3), 4)- то, что протекает, имеет место быть. Суммарные, итоговые уравнения (1), (2), (3), (4)- выражают лишь баланс, итог. Нельзя говорить, что протекает реакции (1), (2)..., протекают только стадии 1), 2)...В рамках теории многомаршрутных реакций для количественного описания химического превращения необходимо и достаточно выбрать лишь линейно-независимые маршруты. Правило фаз (3.1.1) определяет их количество. В нашем случае их два и удобно взять первый и второй . Они выражают промышленно важные процессы синтеза метанола и обратной реакции конверсии оксида углерода.

Р= S-I                                           (3.1.1)

Где S-общее число стадий;

I - число независимых промежуточных соединений;

P - число линейно-независимых маршрутов. 

В рамках многомаршрутной реакции не имеет смысла вопрос «образуется ли метанол по реакции (1) или (3)». 

В. М. Померанцевым было выведено кинетическое уравнение синтеза метанола, при условии, что  концентрации двуокиси углерода и водяного пара малы и скорость превращения по второму маршруту незначительна:

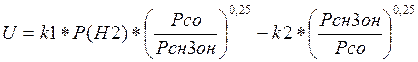          (3.1.2)

Где  U- наблюдаемая скорость реакции;

P(H₂), Р(СО), P(CH₃OH) - парциальные давления реагентов;

k1, k2 - константы скорости реакции в прямом и обратном направлении.

В явном виде кинетическое уравнение было получено  в 1963 году и позже подтверждено в ряде работ[5].

3.2 Равновесие реакции синтеза метанола

Равновесие реакции синтеза метанола долго не могла получить (молекула метанола находится в ассоциативном состоянии),  которое бы отвечало экспериментальным данным. Томас – Потальский и Темкин получили эти уравнения.

Уравнение Темкина с сотрудниками [5]:

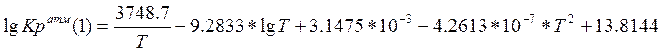    (3.2.1)

Уравнение Томаса – Портальского:

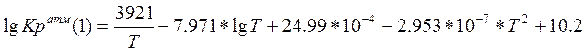                (3.2.2)

где Т- температура (К).

Константу равновесия можно получить различными методами. Один из них – метод приведенных температур и давлений – была получена константа равновесия на основе уравнения Темкина сотрудниками на кафедре:

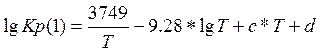        (3.2.3)

Коэффициенты a и b в уравнении (3.2.3) регулярно изменяются с ростом давления газа. Для условий промышленного производства метанола в таблице (3.2.1)  приведены значения коэффициентов[6].

Таблица 3.2.1 - Значения коэффициентов с,d,a,b при разном давлении

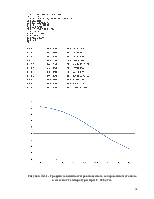
С помощью программы расчета равновесного содержания продукта, составленной на языке BASIC,  получены данные и построены графики зависимости равновесных концентраций метанола от температуры (рисунок).

Для расчета равновесной концентрации реакции синтеза метанола используется следующий состав газа: Н₂    -  70%; СО -  17%; СН₃ОН- 0,2 %

 Программа расчета равновесного содержания метанола

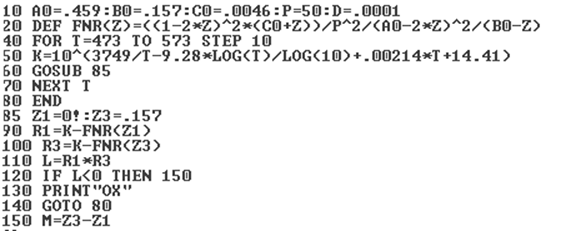
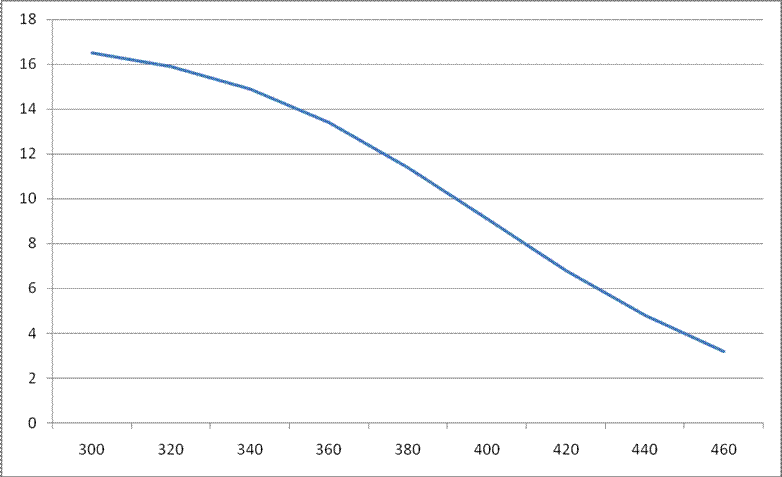
Рисунок 3.2.1 - График зависимости равновесного содержания метанола в смеси от температуры при Р=320 атм.

С увеличением температуры равновесная концентрация продукта падает, это связано с тем, что реакция идет с выделением тепла, реакция экзотермична.

3.3      Оптимальный температурный режим синтеза метанола

Температурный  режим проведения химического процесса, обеспечивающий экономически целесообразную максимальную производительность единицы объема реактора (интенсивность) по целевому продукту, называют оптимальным.

Реакция синтеза метанола является обратимой и идет с выделением тепла.

Скорость химической реакции:

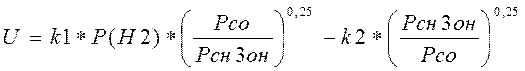                                (3.3.1)

Где k1,k2 - константы скорости прямой и обратной реакции.

Pн₂, Рсо, Рсн₃он - парциальные давления реагентов.

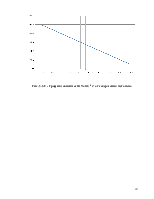
Для экзотермических реакций наблюдаемая   зависимость скорости реакции U от Т изображенная на рисунке 3.3.1:

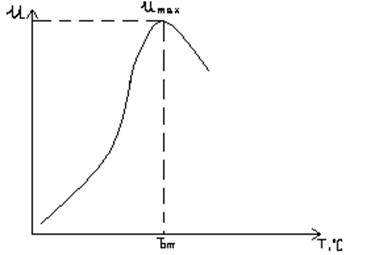
Рисунок 3.3.1 - Зависимость скорости реакции от температуры в экзотермических реакциях

Зависимость имеет экстремальный характер, есть температура, при которой скорость реакции имеет максимальное значение.

Для нахождения Топт. берем производную скорости по температуре:

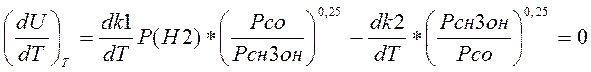                 (3.3.2)                                        

Или 

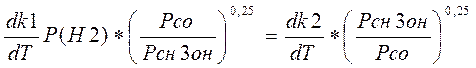                                   (3.3.3)                                        

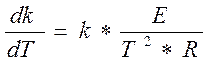                                                                                      (3.3.4)

Т.к. по уравнению Аррениуса

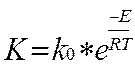
(3.3.5)

то 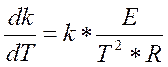                                                                                         (3.3.6)

т.е. 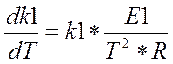                                                                                      (2.3.7)        

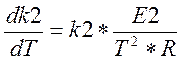                                                                                   (3.3.8)

Где k₀- предэкспонентциальный множитель;

R=8.31441 Дж/(К*моль) -газовая постоянная;

T-температура, К.

После всех преобразований получаем уравнение:

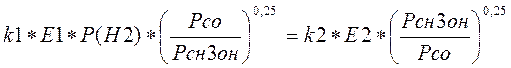                                   (3.3.9)

Из термодинамики известно, что kp= (k1/k2)^v, где v- стехиометрическое