Определение движения груза, амплитуды, частоты и периода колебаний материальной точки, страница 2

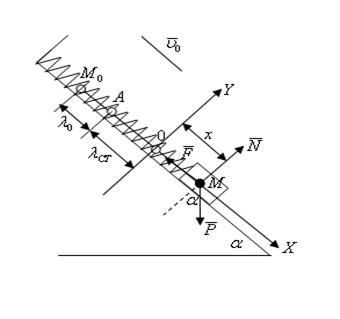
За начало координат примем положение статического равновесия 0.

А- конец недеформированной пружины, тогда 0А=- статическая деформация, которой соответствует сила упругости .

Рассмотрим условие статического равновесия груза без учета сопротивление:

т.к 

, таим образом,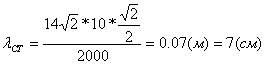

Изобразим груз в промежуточном положении М.На основании закона Гука:

 так как , то

Составляем дифференциальное уравнение движения груза:

, где - проекция сил на ось X, действующих на груз, - ускорение груза, очевидно,

 

Обозначим , где - частота, .

Перепишем ДУ:  - это дифференциальное уравнение второго порядка, характеристическое уравнение имеет комплексные корни, следовательно, его решением будет зависимость: ,                                                (1)

 где- произвольные постоянные, зависящие от начальных условий.

В начальный момент времени груз находился в положении , значит,

 . Начальная скорость

Продифференцируем уравнение (1), получим                  (2)

Подставив в уравнения (1) и (2) (начальный момент времени) и начальные условия, получим

 и

Уравнение движения груза можно записать так:

Амплитуда колебаний:

Период колебаний:

Значение силы упругости максимально при наибольшей деформации пружины, очевидно

, поэтому

Уравнение движения груза, м	Амплитуда колебаний, м	Частота колебаний,	Период колебаний, с	Наибольшее значение модуля силы упругости, Н
	0.25	10