Определение расчетных гидрологических характеристик, используя методы теории вероятности и математической статистики, страница 2

1.2.Построение математической и эмпирической  кривых обеспеченности

Для построения нужно рассчитать до конца таблицу 1.1, а именно вычислить (k_i-1) – отклонение от среднего, а так же (k_i-1)² и (k_i-1)³. Нужно убедиться в том, что ∑(k_i-1)=0.

·  P_эмп – эмпирическая обеспеченность, %: Р_эмп=(i/(n+1))*100%;

·  C_V – коэффициент вариации: 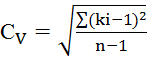 = 0,33;

·  C_S – коэффициент асимметрии:  = 0,44.

Найдём отношение C_S/C_V=1,33 таким образом нашему гидрологическому явлению (среднегодовому расходу) соответствует трехпараметрическое гамма-распределение. Для нахождения ординат математической кривой обеспеченности примем C_S=C_V , тогда можно воспользоваться таблицей, приведенной в приложении 2: Канарский Н.Д., Михалев М.А. Гидрологические расчёты: Учеб. пособие Л.: Изд-во Политехнический Институт имени М.И. Калинина, 1984. 62с. Данные значения записывают в таблицу 1.3, где для значений обеспеченности Р представлены модульные коэффициенты Kт и далее строится математическая кривая обеспеченности, а так же наносятся эмпирические точки из таблицы 1.

·  m_k=0,1 – масштаб интервала;

·  m_Pk=4% - масштаб вероятности.

Вывод: принята математическая кривая обеспеченности соответствующая трехпараметрическому гамма распределению, при C_V=0,33; C_S/C_V=1; Qср.=18,59 м³/с для р. Сок.

2.Определение расчетных гидрологических характеристик при недостаточности данных наблюдений на примере реки Б. Черемшан:

2.1.Обоснование выбора реки – аналога. В качестве реки аналога р. Сок

В тех случаях, когда величина  относительной среднеквадратической ошибки нормы изучаемой гидрологической характеристики оказывается больше 10%, продолжительность периода наблюдений считается недостаточной. В этих случаях прибегают к удлинению рядов наблюдений.

Основным способом удлинения рядов наблюдений гидрологических расчетных характеристик является метод аналогий. Применение его возможно при наличии  совместных рядов наблюдений на изучаемой реке и  реке-аналоге, для которой продолжительность периода наблюдений должна быть достаточна. При выборе реки аналога принято учитывать следующие условия:

1.  возможную географическую близость расположения водосборов;

2.  сходство климатических условий;

3.  однородность условий формирования стока, однотипность подстилающей поверхности, по возможности близкую степень озерности, залесенности, заболоченности и распаханности;

4.  площади водосборов должны отличаться не более, чем в 10 раз, а их средние высоты (для горных рек) – не более, чем на 300 м;

5.  отсутствие факторов, существенно искажающих величину естественного речного стока (регулирование стока, сбросы, изъятия их на орошение и другие нужды);

6.  число лет совместных наблюдений n должно быть не менее 10.

С целью отыскания зависимости между случайными величинами используется метод прямолинейной регрессии с вычислением коэффициента корреляции, позволяющий оценить меру связи между величинами и подобрать параметры уравнения, эту  связь описывающие.

Для реки Б. Черемшан, расположенной в том же районе, что и река Сок, известны среднегодовые расходы за 7 лет, одновременно наблюдавшееся с расходами реки Сок. Так  же известны для реки Б. Черемшан среднемесячные расходы за трехлетний период наблюдений. Таким образом, можно рассчитать ещё за 3 года среднегодовые расходы. Расчет приведен в таблице 2.1.

·  Q_i – среднегодовой расход, м³/с: Q_i=∑Q_j/12 (Q_j – среднемесячный расход).

Теперь, имея 10 лет совместных наблюдений среднегодовых расходов можно сосчитать коэффициент корреляции τ_xy рассчитав таблицу 2.2.

·   – средний расход за десятилетний период для аналога (р. Сок), м³/с: =∑Qa_i/10=192,1/10=19,21 м³/с;

·   - средний расход за десятилетний период для данной реки (Б. Черемшан), м³/с: =∑Qi/10=186,6/10=18,66 м³/с;

·   – коэффициент корреляции: 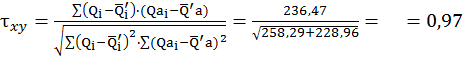 (условие  выполнено).

Далее рассчитаем коэффициент регрессии и его среднеквадратичную ошибку :

· 

· 

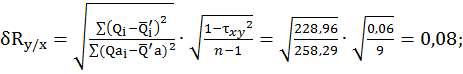
·  тогда отношение:  (условие  выполнено).

Вывод:  река Сок удовлетворяет всем условиям и может быть принята как река-аналог для реки Б. Черемшан.

2.2.Приведение ряда среднегодовых расходов реки Б. Черемшан к ряду достаточной длины

Составим зависимость для нахождения расхода реки Б. Черемшан в любой год:

·  ;

·  ;