







Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Уфа
Хронологический ряд измеренных гидрологических величин представляет простую статистическую совокупность, на основании соответствующей обработки которой можно построить статистический ряд.
В гидрологических расчётах принято использовать нормированные значения величин, которые называются модульными коэф-ми К и определяются по ф-ле:
К=Qi/Qср
Весь диапазон изменения модульных коэф-ов от Кmax до Кmin делим на интервалы, число которых S определим по ф-ле:
![]() , где n-общее число измерений (n=25)
, где n-общее число измерений (n=25)
![]()
Длину интервала определим по ф-ле:
![]()
Далее вычисляем значения модульных коэф-в на границах интервала, подсчитываем кол-во величин m из хронологического ряда, попадающих в каждый интервал. Поделив m на число наблюдений (25), получим относительную частоту.
Все расчёты представлены в таблице 2. Графическое изображение статистического ряда - это гистограмма (или ступенчатый график распределения частот). См рис.3.
В гидрологических расчёта применяется понятие обеспеченности - Р - вероятность превышения заданной величины. (см табл.2). Зависимость между случайной величиной и её обеспеченностью называется кривой обеспеченности. Откладывая против середины каждого интервала обеспеченность получим ступенчатый график, который называется статистическим графиком обеспеченности (рис. 3). При n→∞ гистограмма и ступенчатый график обеспеченности будут стремиться к некоторым математическим кривым (см. рис 3.): 1-дифференциальной функции распределения; 2 - математической кривой обеспеченности.
3.Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Уфа
Выбор аналитической кривой обеспеченности, отвечающей анализируемым данным гидрометрических наблюдений, начинается с построения эмпирической кривой (рис.4), координаты которой определяются значениями модульных коэффициентов К и соответствующих им эмпирических обеспеченностей Рэмп, вычисляемых для гидрологических величин по формуле:
Рэмп= i/(n+1), где i - порядковый номер в ранжированном ряду, где гидрологические величины представлены в убывающем порядке, см. таблицу 3.
Гидрологическим явлением отвечают, как правило, асимметричные кривые распределения плотностей вероятности, поэтому аналитические кривые обеспеченности для них будут определяться следующими параметрами: коэффициентами вариации Сv и асимметрии Сs. Т. к. кол-во n-ограничено, то смещённые (неточные) оценки параметров находятся из формул:
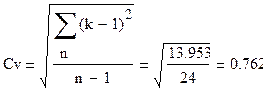
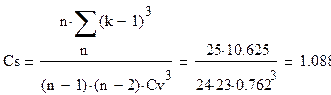
Смещение обуславливается малым сроком наблюдений n и зависит от отношения Сs/Сv.
![]()
По данным таблицы в [1] стр.58 строим плавную аналитическую кривую (см. Приложение 1). Погрешности вычисления Сs и Сv определим по формуле:
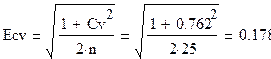
![]()
Для сближения математической и эмпирической кривых проанализируем таблицы на стр.58 в [1]. Построим математическую кривую при Сv=1 (см.рис 4.)
4. Определение коэффициента корреляции между максимальными наблюденными расходами рек Ай и Уфа
В тех случаях, когда величина относительной среднеквадратической ошибки нормы изучаемой гидрологической характеристики оказывается больше 10%, продолжительность периода наблюдений считается недостаточной. В этих случаях прибегают к удлинению рядов наблюдений. Основным способом удлинения ряда наблюдений гидрологических расчетных характеристик считается метод аналогий. Применение его возможно при наличии совместных рядов наблюдений на изучаемой реке и реке - аналоге, на которой продолжительность периода наблюдений д. б. достаточна. При выборе реки- аналога необходимо учитывать условия, приведенные в [2] на стр. 17.
При применении метода аналогий необходимо найти уравнение связи между гидрологическими величинами (расходами) изучаемой реки и реки - аналога
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.