Назначение лабораторных установок и правила оформления отчетов. Обработка результатов измерений в физическом практикуме, страница 3

            Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более

Среднее значение полной погрешности складывается из случайной и систематической погрешностей.

            Ответ с учетом систематических и случайных ошибок записывается в виде

ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ

            В физических экспериментах чаще бывает так, что искомая физическая величина сама на опыте измерена быть не может, а является функцией других величин, измеряемых непосредственно. Например, чтобы определить объём цилиндра, надо измерить диаметр D и высоту h, а затем вычислить объем по формуле

Величины D и h будут измерены с некоторой ошибкой. Следовательно, вычисленная величина V получится также с некоторой ошибкой. Надо уметь выражать погрешность вычисленной величины через погрешности измеренных величин.

Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку.

Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.

Пусть искомая величина φ является функцией нескольких переменных Х, У, Z…

φ(Х, У, Z…).

Путем прямых измерений мы можем найти величины , а также оценить их средние абсолютные ошибки … или средние квадратичные ошибки s_Х, s_У, s_Z…

Тогда средняя арифметическая погрешность Dj вычисляется по формуле

где  - частные производные от φ по Х, У, Z. Они вычисляются для средних значений …

Средняя квадратичная погрешность вычисляется по формуле

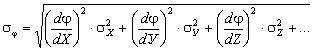
Пример. Выведем формулы погрешности для вычисления объёма цилиндра.

а) Средняя арифметическая погрешность.

Величины D и h измеряются соответственно с ошибкой DD и Dh.

Погрешность величины объёма будет равна

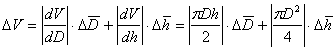
б) Средняя квадратичная погрешность.

Величины D и h измеряются соответственно с ошибкой s_D, s_h.

Погрешность величины объёма будет равна

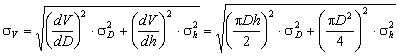
Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять относительную погрешность. Для этого (в случае средней арифметической погрешности) надо проделать следующее.

1. Прологарифмировать выражение.

2. Продифференцировать его.

3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.

4. Взять выражение перед различными дифференциалами по модулю.

5. Заменить значки дифференциалов d на значки абсолютной погрешности D.

В итоге получится формула для относительной погрешности

Затем, зная e, можно вычислить абсолютную погрешность Dj

Dj = j×e

Пример.