













Предварительная оценка вида распределения результатов измерения
Для предварительной оценки вида распределения по полученным данным строят гистограмму распределений или полигон распределения. Вначале производится группирование – разделение данных от наименьшего xmin до наибольшего xmax на r интервалов. Для количества измерений от 30 до 100 рекомендуемое число интервалов 7–9. Ширину интервала выбирают постоянной для всего ряда данных, при этом следует иметь в виду, что ширина интервала должна быть больше погрешности округления при записи данных. Ширину интервала вычисляют по формуле
![]() , где r – число интервалов.
, где r – число интервалов.
Установив границы интервалов, подсчитывают число результатов измерений, попавших в каждый интервал. При построении гистограммы и полигона распределения масштаб этих графиков рекомендуется выбирать так, чтобы соотношение высоты графика (А) к его основанию (В) было примерно 3 : 5.
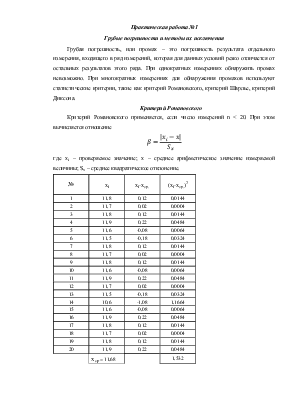
Результаты измерений:
|
xi |
xi-xср. |
(xi-xср.)2 |
|
|
1 |
11,8 |
0,15667 |
0,024545 |
|
2 |
11,7 |
0,05667 |
0,003211 |
|
3 |
11,8 |
0,15667 |
0,024545 |
|
4 |
11,9 |
0,25667 |
0,065879 |
|
5 |
11,6 |
-0,04333 |
0,001877 |
|
6 |
11,5 |
-0,14333 |
0,020543 |
|
7 |
11,8 |
0,15667 |
0,024545 |
|
8 |
11,7 |
0,05667 |
0,003211 |
|
9 |
11,8 |
0,15667 |
0,024545 |
|
10 |
11,6 |
-0,04333 |
0,001877 |
|
11 |
11,9 |
0,25667 |
0,065879 |
|
12 |
11,7 |
0,05667 |
0,003211 |
|
13 |
11,5 |
-0,14333 |
0,020543 |
|
14 |
11,6 |
-0,04333 |
0,001877 |
|
15 |
11,9 |
0,25667 |
0,065879 |
|
16 |
11,8 |
0,15667 |
0,024545 |
|
17 |
11,7 |
0,05667 |
0,003211 |
|
18 |
11,8 |
0,15667 |
0,024545 |
|
19 |
11,9 |
0,25667 |
0,065879 |
|
20 |
11,6 |
-0,04333 |
0,001877 |
|
21 |
11,5 |
-0,14333 |
0,020543 |
|
22 |
11,8 |
0,15667 |
0,024545 |
|
23 |
11,7 |
0,05667 |
0,003211 |
|
24 |
11,8 |
0,15667 |
0,024545 |
|
25 |
11,6 |
-0,04333 |
0,001877 |
|
26 |
11,9 |
0,25667 |
0,065879 |
|
27 |
11,7 |
0,05667 |
0,003211 |
|
28 |
11,5 |
-0,14333 |
0,020543 |
|
11,71786 |
0,636592 |
Определяем ширину интервала: ![]()
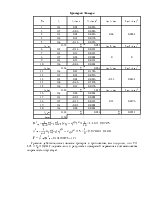
Строим гистограмму распределений, подсчитав число экспериментальных данных, попавших в каждый интервал.
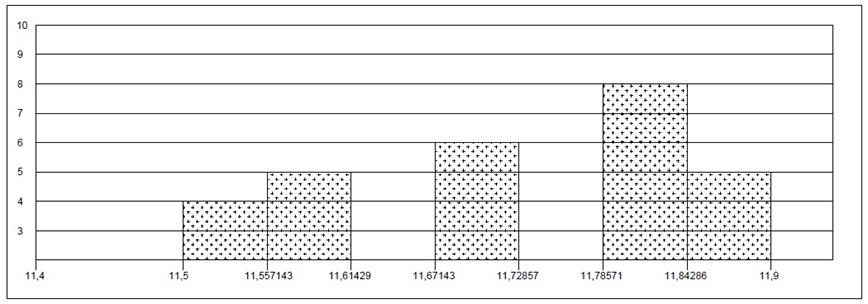
Далее строим полигон распределения, который представляет собой кусочно-линейную аппроксимацию искомой функции плотности распределения результатов измерения.
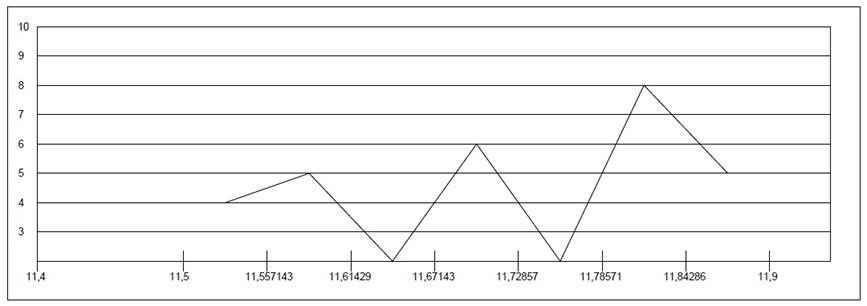
Нормальный закон распределения, называемый часто распределением Гаусса, описывается зависимостью:σ π
![]() , где σ –
параметр рассеивания распределения, равный среднему квадратическому отклонению.
, где σ –
параметр рассеивания распределения, равный среднему квадратическому отклонению.
При количестве измерений n < 10 проверить гипотезу о виде распределения результатов измерения невозможно. При числе данных 10 < n < 50 также трудно судить о виде распределения. Поэтому для проверки соответствия распределения данных нормальному распределению используют составной критерий. Если гипотеза о нормальности отвергается хотя бы по одному из критериев, считают, что распределение результатов измерения отлично от нормального.
Критерий I. Вычисляют значение d по формуле:
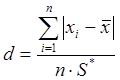 , где S* - смещенное СКО.
, где S* - смещенное СКО.
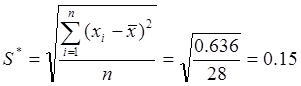
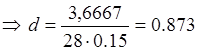
Гипотеза о нормальности
подтверждается, если ![]() , где d1-q
и dq — процентные точки распределения значений d,
которые находятся по таблице. При числе измерений n=28 d1-q=0,71,
dq=0,88. 0,71<0.873<0,88 - гипотеза о нормальном
распределении подтверждается.
, где d1-q
и dq — процентные точки распределения значений d,
которые находятся по таблице. При числе измерений n=28 d1-q=0,71,
dq=0,88. 0,71<0.873<0,88 - гипотеза о нормальном
распределении подтверждается.
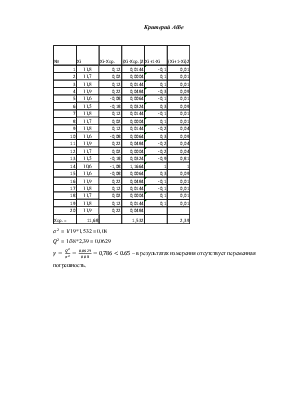
Критерий II.
Гипотеза о нормальности распределения результатов измерения подтверждается,
если не более m разностей ![]() превзошли
значения
превзошли
значения ![]() .
.
Здесь ![]() ;
; ![]() — верхняя
— верхняя ![]() - процентная
точка нормированной функции Лапласа. Значения доверительной вероятности Р
выбирают из таблицы.
- процентная
точка нормированной функции Лапласа. Значения доверительной вероятности Р
выбирают из таблицы.
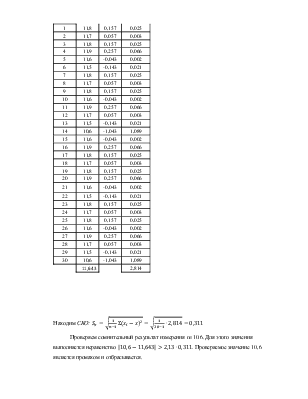
Найдем СКО S
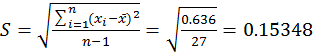 ,
,
Выбрав уровень значимости q = 0,05 для n =28 из таблицы, найдем Р = 0,972. Из таблицы определим zp/2 = 2,195. Тогда:
![]()
Ни одно отклонение ![]() не превосходит S*zp/2, это говорит о том
что гипотеза о нормальном распределении данных подтверждается.
не превосходит S*zp/2, это говорит о том
что гипотеза о нормальном распределении данных подтверждается.
Практическое занятие № 4
Классы точности средств измерений
К.Т. – обобщенная характеристика средства измерения, выраженная пределами допускаемых значений его основной и допустимой погрешности.
Основная погрешность регламентируется у средства измерения при нормальных условиях (t = 200C)
Если условия отличаются от нормальных, то регламентируются дополнительные погрешности. Дополнительная погрешность указана в тех. документации средства измерения, если нет, то ∆доп. = ∆осн..
∆ = ∆осн. + ∆доп.
Пределы допускаемой основной погрешности выражают в форме абсолютной, приведенной и относительной погрешностей.
1). Пределы допускаемой основной абсолютной погрешности устанавливаются по формуле:
1. ∆ = ![]() ;
;
2. ∆ = ![]()
В тех. документации классы точности в форме абс. погрешности обозначаются прописными латинскими буквами или римскими цифрами, при этом меньшие пределы соответствуют букве, ближней к началу алфавита, т.е. А точнее, чем Б.
2). В форме приведенной погрешности
Пределы допускаемой основной приведенной погрешности устанавливаются так:
ỳ = ![]() ∆/xn
* 100%, где xn
- нормирующее значение, постоянное для всего диапазона измерений. За
нормирующее принимают больший из 2-х пределов измерений, но есть исключения:
∆/xn
* 100%, где xn
- нормирующее значение, постоянное для всего диапазона измерений. За
нормирующее принимают больший из 2-х пределов измерений, но есть исключения:
а). для средств измерений, шкала которых имеет условный ноль:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.