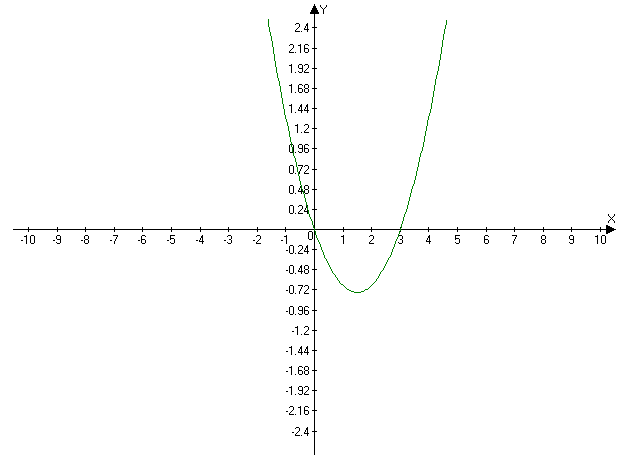
II. Исследовать и построить график функции 
.
Решение.
1) Область определения данной
функции 
;
2) Для выяснения четности и
нечетности функции рассмотрим 
. 
- функция общего вида и график
никакой симметрии относительно осей не имеет. Функция периодическая;
3) Вертикальных асимптот нет
4)Найдем наклонные асимптоты,
вычислив 
и 
(при
раскрытии неопределенностей типа 
будем использовать
правило Лопиталя): 
, следовательно, функция не имеет наклонных ассимптот;
5) Исследуем функцию на экстремум и найдем её интервалы
монотонности. 
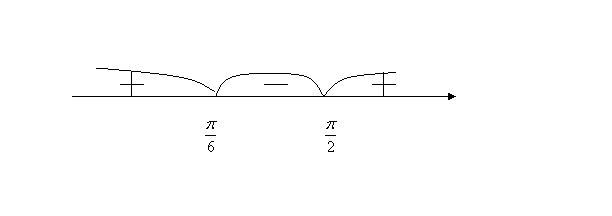
Функция возрастает на промежутке 
и убывает
на промежутке 
.
6) Найдем интервалы выпуклости и вогнутости графика кривой и точки перегиба:
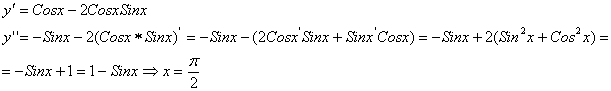
Критические точки второго
рода: 
( 
).
Учитывая, что график функции 
(x) убывает на
промежутка и
возрастает на промежутке 
можно сделать
вывод, что график исходной кривой выпуклый при и вогнутый при
. Точки с
координатами 
и 
являются точками
перегиба.
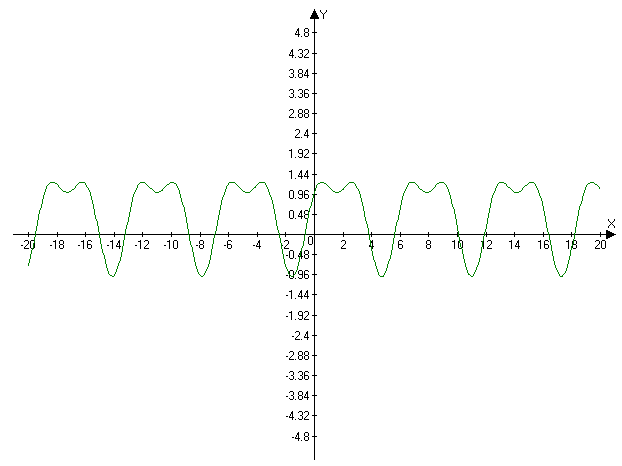
7)Для построения графика
функции используем следующие значения функции: f(12)
=0,175; f(11)=-0,999; f(10) =0,160;
f(9)=1,242; f(8)=1,01; f(7)=1,225;
f(6)=0,642; f(5)=-0,878;
f(4) =-0,325; f(3) =1,121; f(2)=-1,082;
f(1)=-1,133; f(0)=1; f(-12)
=1,248; f(-11)=1,00001; f(-10)
=1,248; f(-9)=0,418; f(-8)=-0,968;
f(-7)=-0,088; f(-6)=1,201;
f(-5)=1,039; f(-4) =1,184;
f(-3) =0,838; f(-2)=-0,736;
f(-1)=-0,549. Построенный график функции имеет вид:
III.Решить задачу с помощью производной
Из всех прямоугольников данной площади S определить тот периметр, которого наименьший.
Решение
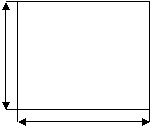
Площадь прямоугольника: S=xy
|
Выразим сторону y через
площадь :
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.