Функция рабочего затухания для фильтра с максимально плоской характеристикой описывается выражением
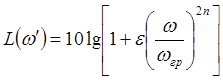 , дБ, где
, дБ, где 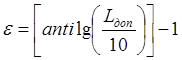 ,
,
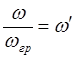 - нормированная
частота.
- нормированная
частота.
Функция рабочего затухания для фильтра с чебышевской характеристикой затухания имеет вид
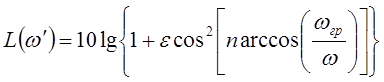 , при
, при ![]()
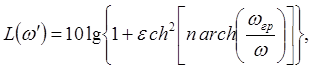 при
при ![]() , где
, где 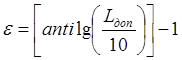 .
.
На рисунках а), б) показаны максимально плоские рабочие характеристики фильтров низких и высоких частот; на рисунках б) и в) – чебышевские рабочие характеристики затухания полосовых и детекторных фильтров.
Методы расчета фильтров.
Существует много методов расчета фильтров. Основными из них являются два метода: практический метод и общий метод – метод расчета фильтров по их рабочим характеристикам.
Первый метод расчета предусматривает построение фильтра из определенных элементов – четырехполюсников с помощью их каскадного соединения, то есть лестничных фильтров. Составляющие фильтр четырехполюсники должны иметь одинаковые частоты и одинаковые сопротивления в точках сочленения, а также согласованны с нагрузкой и генератором. Расчет простой. При выполнении указанных требований постоянная передача фильтра равна сумме постоянных передач, передачи отдельных элементов.
Однако большое число ограничений не позволяет получить фильтры с оптимальными частотными характеристиками, содержащих малое число элементов.
Второй метод – общий метод синтеза по рабочим параметрам свободен от
недостатков первого и в настоящее время получил наибольшее распространение. В
качестве исходных данных задаются: вид функции рабочего затухания (максимально
плоская или чебышевская), граничные частоты ![]() или
или ![]() ,
, ![]() ,
допустимые потери в полосе прозрачности.
,
допустимые потери в полосе прозрачности. ![]() .
.
Основой расчета являются фильтры-прототипы нижних частот. Фильтр-прототип нижних частот может быть реализован в одном из двух вариантов схем, приведенных на рисунке.
Переход от обычного фильтра нижних частот к фильтру – прототипу нижних частот осуществляется с помощью перехода от действительной частоты к нормализированной (изменение масштаба частоты)
![]() , где
, где 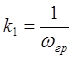 .
.
При таком выборе масштаба по оси частот граничная частота нормализованного
фильтра всегда равна 1. Величена внутреннего сопротивления генератора ![]() также нормируется к 1.
также нормируется к 1.
Схема фильтра-прототипа имеет вид
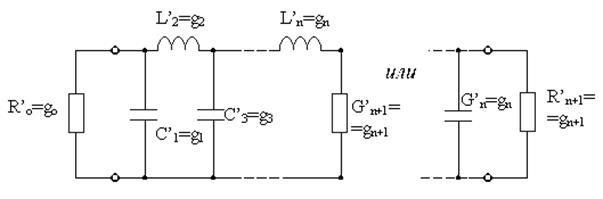
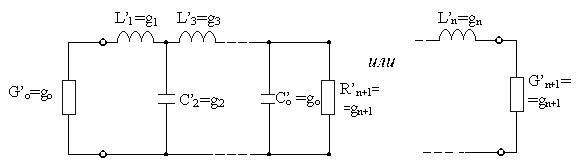
Рис. Возможные варианты схем фильтра-прототипа.
Обозначения имеют следующий смысл:
![]() - индуктивность последовательной катушки и
емкость параллельного конденсатора.
- индуктивность последовательной катушки и
емкость параллельного конденсатора.
![]() - сопротивление генератора
- сопротивление генератора ![]() , если
, если ![]() , или
проводимость генератора
, или
проводимость генератора ![]() , если
, если ![]() ;
;
![]() - сопротивление нагрузки
- сопротивление нагрузки ![]() , если
, если ![]() , или
проводимость нагрузки
, или
проводимость нагрузки ![]() , если
, если ![]() .
.
При переходе к нормализированной частоте величины элементов нормируются
так, чтобы ![]() и
и ![]() .
Приведенная схема фильтра-прототипа предусматривает нагрузку фильтра с правой и
левой стороны на чисто активные нагрузки. Если нагрузки комплексные, то их
мнимые части включаются в ближайший к ним элемент фильтра. Переход от
нормированных фильтров-прототипов к другим значениям сопротивлений и
действительной шкале частот осуществляется с помощью следующих преобразований
элементов цепи: для активных сопротивлений и проводимостей
.
Приведенная схема фильтра-прототипа предусматривает нагрузку фильтра с правой и
левой стороны на чисто активные нагрузки. Если нагрузки комплексные, то их
мнимые части включаются в ближайший к ним элемент фильтра. Переход от
нормированных фильтров-прототипов к другим значениям сопротивлений и
действительной шкале частот осуществляется с помощью следующих преобразований
элементов цепи: для активных сопротивлений и проводимостей
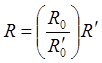 или
или 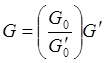 , для индуктивностей
, для индуктивностей
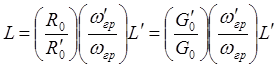
для емкостей
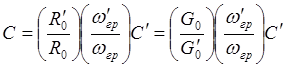 .
.
Обычно значения параметров фильтров прототипов ![]() приводятся
в справочниках, например такие таблицы есть в книге [ ].
Требуется только задать число элементов фильтра
приводятся
в справочниках, например такие таблицы есть в книге [ ].
Требуется только задать число элементов фильтра ![]() и
и ![]() для каждой из структур, приведенных на рисунке.
для каждой из структур, приведенных на рисунке.
Фильтр верхних частот.
В этом случае для перехода к нормализованной частоте ![]() следует произвести преобразование (замену
частотной переменной)
следует произвести преобразование (замену
частотной переменной)
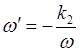 .
.
Такая замена возможна для четной функции. Функция вносимых потерь
является четной относительно ![]() и
и
![]() .
.
Замена такого вида эквивалентна перемене местами начала координат и бесконечно удаленной точки, а также замене положительной оси частот отрицательной. На рисунке показано такое преобразование
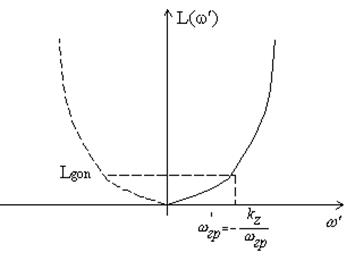
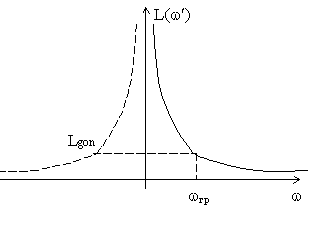
Рис.
Нормализированный фильтр нижних частот. Фильтр верхних частот.
Как видно из рисунка для получения ![]() следует
принять
следует
принять ![]() .
.
При таком преобразовании приходим к обращенным схемам фильтра, в которых последовательными элементами являются конденсаторы, а параллельными индуктивности и для фильтра верхних частот, получаемого из фильтра-прототипа следует находить индуктивности и емкости как
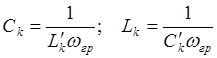 .
.
Эквивалентная схема фильтра верхних частот имеет вид, показанный на рисунках
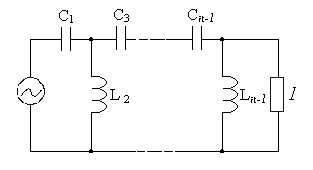
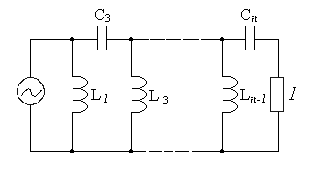
Рис.
Полосовой фильтр.
Для получения полосы пропускания, заключенной в пределах граничных частот
![]() и
и ![]() следует
перейти от переменной
следует
перейти от переменной ![]() переменой вида
переменой вида
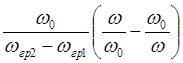 , где
, где ![]() .
.
На рисунке показано такое преобразование, фильтра прототипа в полосовой фильтр.
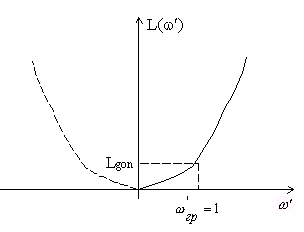
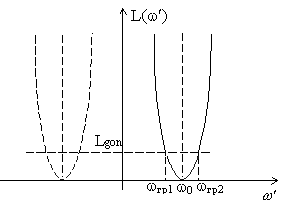
Рис.
Эквивалентная схема полосового фильтра показана на рисунке
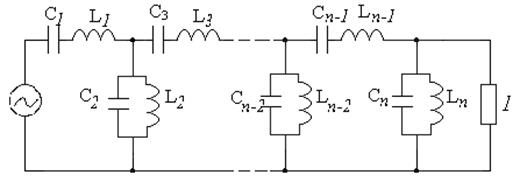
Рис.
Из схемы видно, что индуктивности в фильтре-прототипе при переходе к полосовому фильтру должны преобразовываться в последовательные колебательные контуры, а емкости в параллельные. При этом индуктивности в последовательных контурах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.