Параболические антенны. Диаграмма направленности параболической антенны

4. Параболические антенны

Параболические антенны являются радиотехническим аналогом оптических прожекторов и содержат те же основные элементы, что и прожекторы: точечный (квазиточечный) облучатель, создающий поле а виде сферически волны, и параболический отражатель (зеркало), преобразующий сферическую волну и плоскую (рис. 68, часть I).

Такие антенны относятся к классу плоских синфазных излучателей, поскольку поле в их раскрыве представляет собой плоскую волну и, следовательно, в пределах ракрыва оно синфазно. Амплитудное распределение поля в раскрыве обычно имеет ослабление к краям, что ввязано в основном с формой диаграммы направленности облучателя, Элементарным излучателем раскрыва являются элемент плоского волнового фронта, то есть элемент Гюйгенса.

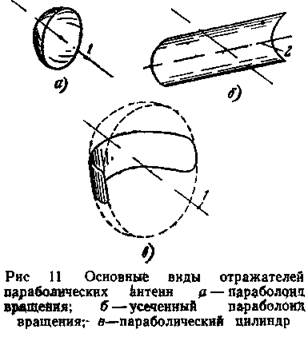
Диаграмма направленности параболической антенны может иметь игольчатую или веерную форму в зависимости, от формы раскрыва антенны. Игольчатая диаграмма образуется, например, зеркалом в форме параболоида вращения с раскрытом круглой формы (рис. 11, а), а веерную диаграмму имеют усеченные параболоиды вращения (рис.11, в) и антенны с зеркалом в виде параболического цилиндра (рис. 11, б). Антенны последнего вида в качестве облучателя должны иметь не точечный, а линейный облучатель, представляющий собой линейную синфазную антенну, расположенную на фокальной оси зеркала и создающую у поверхности зеркала волну с цилиндрическим фронтом. Отражатель же преобразует эту волну в плоскую.

Расчет диаграммы направленности, основанный   на   учете эквивалентных токов в

раскрыве, дает приближенный  результат, справедливый лишь для главного и первых боковых лепестков. Этот метод называют апертурным. Для расчета дальних боковых лепестков и заднего излучения апертурный метод непригоден, и расчет необходимо вести исходя из распределения электрических токов непосредственно на параболическом зеркале. Однако этот метод значительно сложнее и здесь не рассматривается.

Уравнение профиля параболических отражателей в   главном их сечении записывается в виде (рис. 12)

                                                      (22)

-  в декартовой системе координат и

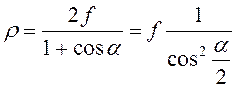                                               (23)

-  в полярной системе координат.

Основные геометрические размеры зеркала,   указанные на рис. 12 (диаметр раскрыва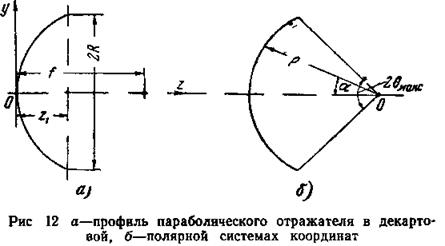

2R, фокусное   расстояние f, глубина зеркала z₁), связаны между собой   соотношением,   следующим из (22) при y=R,

.                                                               (24)

Угол раскрыва 2α_макс (рис. 12б) равен

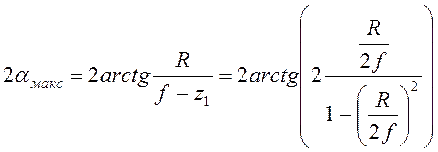.                 (25)

От точности выполнения профиля зеркала зависит величина фазовых искажений в раскрыве Δψ, обусловленных изменением оптической длины некоторых лучей (рис. 13), Как следует из рис. 13, изменение длины пути связано с допуском на изготовление профиля зеркала Δρ соотношением

,

Из последней формулы видно, что при одном и том же заданном допуске Δρ фазовые искажения получаются на краях зеркала меньшими, чем в центре его. Если заданы допустимые искажения, скажем ΔΨ _доп=π/4, то наиболее жесткий допуск в центре зеркала оказывается равным

.

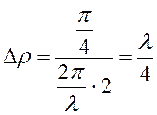Отсюда следует, до допуск становится тем более жестким, чем короче волна.

Конструктивно отражатели параболических антенн могут выполняться как из сплошного, так и из перфорированного металлического листа. Наряду с этим в целях снижения веса и ветровых нагрузок целесообразно применение отражателей сетчатой и решетчатой конструкции. Во всех случаях применения несплошных отражателей размер отверстий или ячеек, а также толщина проводов сетки (решетки), выбираются, исходя из условия минимального допустимого просачивания электромагнитной энергии сквозь  отражатель,   обычно  составляющего   несколько   процентов от энергии, падающей на зеркало.

К облучателям параболических, а также и линзовых, антенн предъявляются требования создания сферической волны (а для параболических цилиндров—цилиндрической волны) и однонаправленного излучения с довольно широкой диаграммой в виде одного основного лепестка. Положение некоторой воображаемой точки, являющейся центром сферического фронта волны облучателя, называют его фазовым центром. Чаще всего фронт волны облучателей совпадает со сферой лишь приближенно.

Оптимальной диаграммой облучателя считают такую, ширина лепестка которой по уровню ~ 10 дБ (примерно 0,3 по полю) равна 2α_макс (рис. 12, б). В этом случае доля энергии, излучаемой мимо зеркала, сравнительно невелика, а распределение энергии в пределах отражателя относительна равномерное. Если диаграмму облучателя сделать более узкой, то края зеркала будут использоваться плохо, и эффективный размер антенны и, следовательно, коэффициент использования поверхности (КИП) окажутся заниженными. С другой стороны, при чрезмерном расширении диаграммы облучателя значительная доля энергии будет излучаться мимо зеркала, а это ослабляет поле в главном направлении и увеличивает боковое и заднее излучение, что также приводит к уменьшению КНД.

Обычно используются зеркала с углом раскрыва в пределах 2α_макс ≈100°÷140°, что и определяет необходимую ширину диаграммы направленности облучателя.

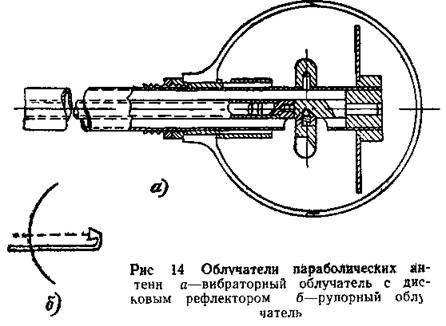
В качестве облучателей из числа малонаправленных антенн чаще всего используются симметричный вибратор с дисковым или вибраторным рефлектором при питании его коаксиальным фидером с применением симметрирующих устройств или открытый конец волновода с небольшим рупором, если тракт питания волноводный. Конструкция и внешний вид этих облучателей показан на рис. 14.

Установка облучателя (точнее его фазового  центра) в фокус должна производиться с определённым допуском, который связал с допустимыми фазовыми искажениями в раскрыве антенны. В зависимости от вида фазовых искажений допуск оказывается разным.