Разработка вариантов железобетонного моста. Расчет балочных пролётных строений моста

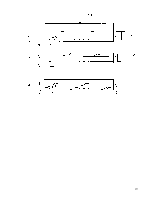
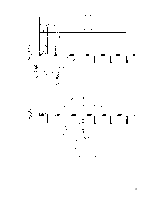
Расчёт на прочность по сжатому бетону между наклонными трещинами.

Условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами:

Где:     - поперечная сила на расстоянии не ближе  от оси опоры;

;

;

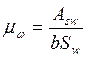 - площадь сечения ветвей хомутов, расположенных в одной плоскости;

 - расстояние между хомутами;

 - рабочая высота сечения.

Для хомутов используем стержневую арматуру периодического профиля А-II d10мм, в одной плоскости расположено два хомута , расстояние между ними вдоль пролётного строения на участке вблизи опоры 15см.

;

;

Условие на прочность удовлетворено с большим запасом.

            Расчёт на прочность по наклонной трещине на действие поперечной силы.

Расчёт производится по условию:

Где:     - сумма проекций усилий всей пересекаемой напрягаемой арматуры на длине проекции трещины C;

 - расчётная поперечная сила, принимаемая над серединой наклонного сечения;

 - сопротивление сжатой хоны бетона срезу.

Длина проекции невыгоднейшего сечения на продольную ось элемента определяется из предположения, что угол наклона трещины к горизонтали составляет . Таким образом С=234см.

>;

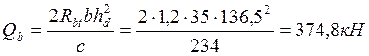Следовательно принимаем .

Трещина пересекает 16 ветвей хомутов . , .

Таким образом:

.

Условие прочности удовлетворено.

Расчёт на действие изгибающего момента.

Условие прочности наклонного сечения по изгибающему моменту:

;

Где:     и  - расстояние от усилий в напрягаемой и ненапрягаемой арматуре до точки приложения равнодействующей усилий в сжатой зоне бетона в сечении, для которого определяется момент.

Расчёт производится для наклонного сечения, начало которого находится у нижней фибры на расстоянии 6м. от опоры непосредственно перед анкером и идёт вверх под наклоном  к горизонтали. Армирование стенки в этой части конструкции производим стержнями периодического профиля класса А-II d10мм. с шагом 20см.

;  ; ; ; ;

 > .

Условие прочности удовлетворено.

Расчёт на трещиностойкость по наклонным сечениям.

Рассмотрим сечение, отстоящее от опоры на 1,5м.

Условие трещиностойкости по главным напряжениям.

;

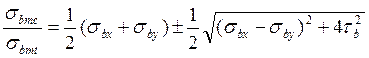Где:     - нормальное напряжение в бетоне вдоль продольной оси от внешней нагрузки и от усилий преднапряжения с учётом потерь;

 - нормальное напряжение в бетоне в направлении, перпендикулярном продольной оси элемента от местной нагрузки;

 - касательное напряжение в бетоне стенки от действия поперечной силы.

Расчётным сечением по высоте балки является сечение, где начинается утолщение (b-min), т.е. отстоящее от верха на 50см.

; ;

; ; ; ;

;

.

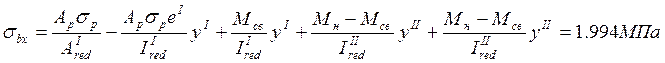
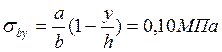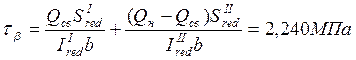Главные сжимающие напряжения <  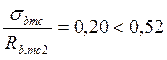следовательно

Ширина раскрытия наклонной трещины определяется по той же формуле, что и нормальной, с разницей лишь а определении растягивающих напряжений в поперечной арматуре стенок балки:

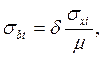
Где:     - напряжение, принимаемое равным  на уровне центра тяжести сечения, ;

 - коэффициент армирования стенки на участке наклонной трещины по направлению главных растягивающих напряжений; его можно определить как отношение проекций площадей всех стержней на нормаль к этому сечению к площади наклонного сечения бетона стенки на этом участке;

 - коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных трещин;

;

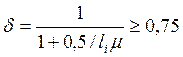 - длина предполагаемой наклонной трещины по направлению, перпендикулярному главным растягивающим напряжениям на участке между крайними по отношению к нейтральной оси рядом арматуры и вутом пояса, наклон трещины тот же, как при расчёте на прочность.

Угол наклона главных напряжений к вертикальной оси сечения определяется из условия:

;  ;

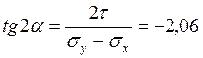Длина наклонной трещины:

.

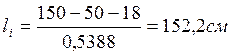Она пересекает 11 ветвей хомутов общей площадью . Кроме того трещина пересекает напряжённую арматуру, площадь которой . Проекции этих площадей на наклонное сечение трещины соответственно:

; .    .

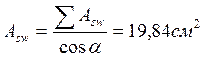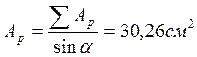Площадь стенки бетона, пересекаемая трещиной . Таким образом коэффициент армирования стенки на участке трещины:

; .

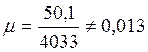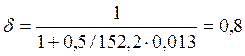Отсюда напряжения в арматуре стенки . Коэффициент раскрытия трещин для стержневой арматуры периодического профиля равен . Радиус армирования определяется из условия:

,

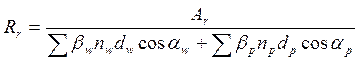Где:     - площадь зоны взаимодействия, равная площади бетона стенки ;

 - для стержней периодического профиля;

 - для пучковой арматуры;

,  - диаметр хомутов и продольных пучков, пересекающих продольное сечение в пределах стенки;

,  - углы наклона хомутов и продольной арматуры к нормали к наклонному