Вариант 955.
Задача 1.
Цепь постоянного тока с одним источником ЭДС представлена на рис. 1.1. Параметры резистивных элементов, величина ЭДС Е и вариант схемы указаны. Требуется определить токи во всех резистивных элементах и проверить полученные результаты с помощью первого или второго законов Кирхгофа.
Схема Д; Е=14 В; R1=R2=1 Ом, R3=R4=9 Ом.
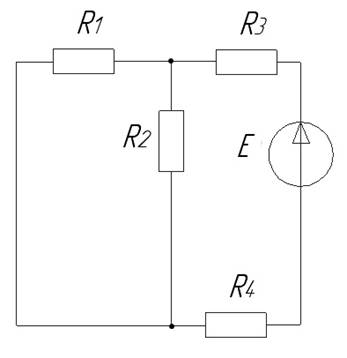
Рис. 1.1.
Решение:
Произвольно выбираем направления токов в ветвях и обозначаем их на схеме (рис. 1.2).
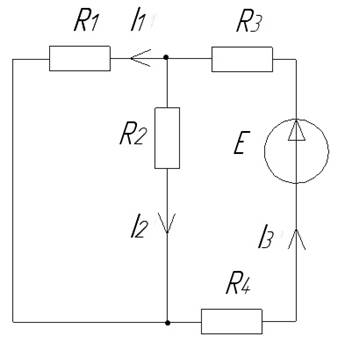
Рис. 1.2.
Преобразуем параллельное соединение сопротивлений 1 и 2 в одно эквивалентное:
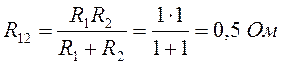
Получили схему, показанную на рис. 1.3.
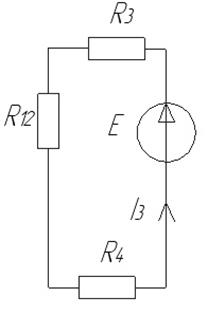
Рис. 1.3.
Находим ток, протекающий через сопротивления 3 и 4:
Напряжение на сопротивлении R12:
Ток через резистор 2:
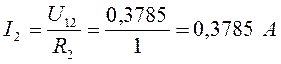
Ток через резистор 1:
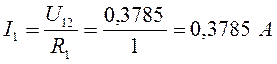
Проверка. Согласно первому закону Кирхгофа, 
.
В нашем случае, 0,3785 + 0,3785 = 0,757 А – токи найдены верно.
Задача 2.
Схема электрической цепи (рис. 2.1) состоит из последовательно соединенных активного R и реактивного Х сопротивлений. Требуется определить параметры R и Х, а также L или С этой цепи, используя дополнительное сопротивление R1, величина которого известна, и только амперметры или только вольтметры электромагнитной системы. Частота f источника питания цепи известна.
Номер схемы 2; I1 = 15 A, I2 = 20 A, I = 32 A, R1 = 3 Ом, f = 450 Гц.
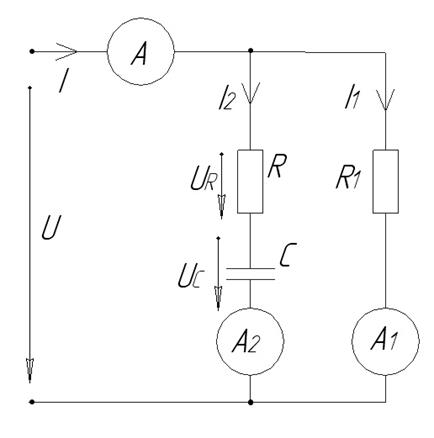
Рис. 2.1.
Решение:
На основании первого
закона Кирхгофа строим векторную диаграмму токов данной цепи. Произвольно
проводим вектор приложенного напряжения, действующее значение которого 
. Вектор тока 
совпадает
по фазе с вектором напряжения, как ток в активном сопротивлении. Из начала
вектора (точка а) описываем дугу радиусом I, а из конца вектора дугу радиусом I2. Пересечение этих двух дуг (точка с) определяет положение
векторов 
и 
на
векторной диаграмме. Из конца вектора 
(точка
е) опускаем перпендикуляр ed на направление вектора и таким
образом разлагаем вектор напряжения на две составляющие: 
, который будет параллелен вектору тока , и 
,
который будет перпендикулярен вектору тока .
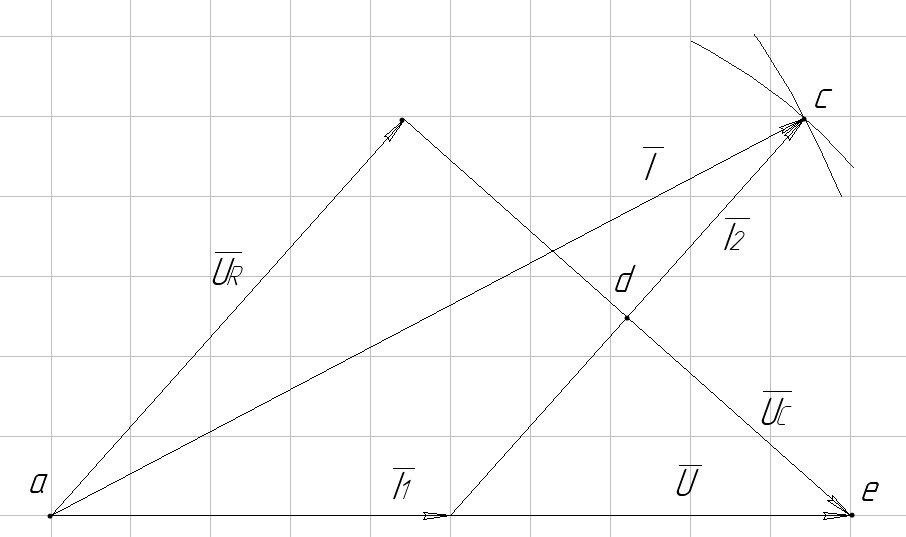
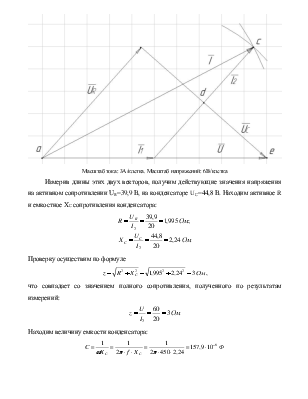
Масштаб тока: 3А/клетка. Масштаб напряжений: 6В/клетка
Измерив длины этих двух векторов, получим действующие значения напряжения на активном сопротивлении UR=39,9 В, на конденсаторе UС=44,8 В. Находим активное R и емкостное ХС сопротивления конденсатора:
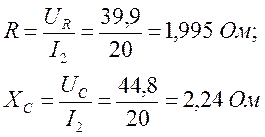
Проверку осуществим по формуле
, что совпадает со значением полного
сопротивления, полученного по результатам измерений:
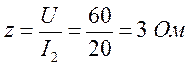
Находим величину емкости конденсатора:
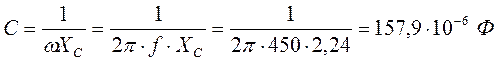
Задача 3.
К электрической цепи, содержащей известное активное сопротивление R, индуктивность L и емкость С (рис. 3.1), приложено синусоидальное напряжение, действующее значение которого U. Частота источника питания схемы f известна. Требуется определить: а) комплексное действующее значение тока I1 в неразветвленной части цепи, а также комплексные действующие значения токов I2 и I3 в параллельно включенных ветвях цепи; б) активную Р, реактивную Q и полную S мощности всей цепи. Задачу решить символическим методом.
Схема 2; U = 50 В; R = 1 Ом; L = 0,35 Гн; С = 176 мкФ; f = 450 Гц.
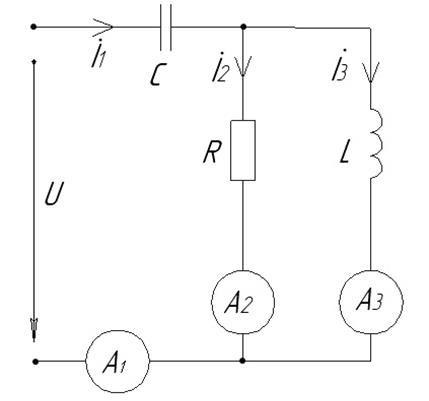
Решение:
а) Для нахождения токов сначала найдем эквивалентное сопротивление электрической цепи.
Комплексные сопротивления ветвей:
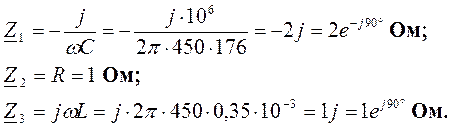
Эквивалентное сопротивление цепи:
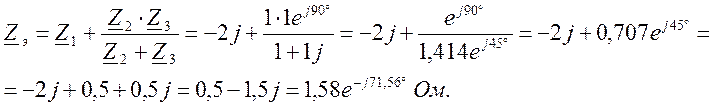
Комплексное
напряжение, принимая начальную фазу за нулевую: 
.
Определяем токи в ветвях. В неразветвленной части цепи:
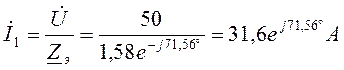
В разветвленной части цепи:
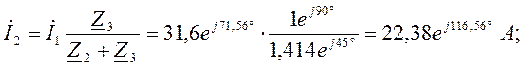
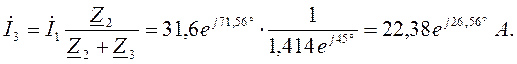
Значение
суммы 
найдено выше при расчете 
.
б) Находим мощности цепи:
Таким образом, Р = 682,6 Вт; Q = –1425 вар; S = 1580 В·А.
Задача 5.
Разветвленная электрическая цепь синусоидального тока, изображенная на рис. 5.1, содержит два источника ЭДС и один источник тока. Параметры источников и сопротивления всех ветвей цепи известны. Требуется: а) преобразовать источник тока в эквивалентный источник ЭДС; б) составить систему уравнений для определения токов во всех ветвях цепи, используя 1-й и 2-й законы Кирхгофа; в) записать полученную систему уравнений в матричной форме.
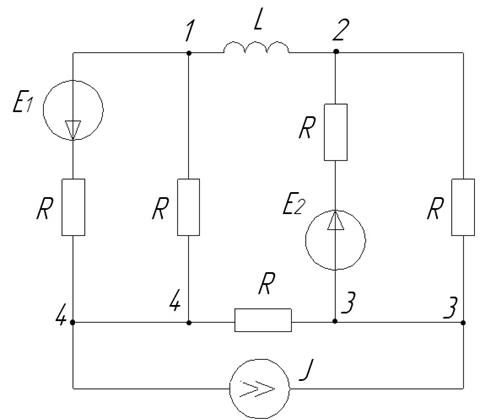
Рис. 5.1.
Решение:
а) Преобразуем источник тока в эквивалентный источник ЭДС:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.