Конструкции и механический расчет проводов марки АС двух цепной воздушной линии электропередач, сооружаемой в населённой местности

Министерство образования РОССИЙСКОЙ ФЕДЕРАЦИИ

СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ ИНСТИТУТ

КОНТРОЛЬНАЯ РАБОТА

По дисциплине: Спец вопросы систем электроснабжения.

Конструкции и механический расчет.

Студент:   Павлов Юрий Алексеевич

Шифр:    01-0016

Курс:  4  

Факультет:     Э.Ф.

Специальность:   10.0400

Проверил преподаватель: Костин В.Н.

Подпись преподавателя:

Боровичи

2003
Задача

Выполнить механический расчёт проводов марки АС сечением F=70 мм² двух цепной(n=2) воздушной линии электропередач напряжением U_ном=110 кВ, сооружаемой в населённой местности.

Климатические условия:      III район по гололёду: максимальная толщина стенки гололёда согласно данным табл. 2.5.3 с. 222 [1] С_max= 15 мм (повторяемость 1 раз в 10 лет);

I  район по скоростному напору ветра:     максимальный напор ветра согласно данным табл. 2.5.1 с. 220 [1] Q_max = 40 даН/ м² (повторяемость 1 раз в 10 лет);

Минимальная температура t_min = - 20^° C; 

Максимальная температура t_max = + 40^° C;

Среднегодовая температура t_ср = - 5^° C.

Решение:

I. Выбор опоры.

На основании исходных данных из приложения 4 с.88 [2] предварительно выбираем промежуточную, двуцепную, железобетонную опору на напряжение 110 кВ типа ПБ110-6. Габаритный пролёт для этой опоры с проводом АС70 составляет l_г = 135м. Геометрические размеры опоры выписываем из приложения 3 с. 86[2]: Н=22,6 м, h_т-п=2,7 м, h_п-з=11,5 м, h_п-п=4,0 м, h_з=3 м.

II. Расчёт удельных нагрузок на провод.

Из таблицы физико-механических характеристик сталеалюминевых проводов (приложение 1 с. 85 [2]) находим вес одного километра провода марки АС70 Р=274 даН/км и диаметр провода марки АС70  d=11,4 мм.

По формулам  6.2-6.9 приведённым на с.62-63 [2] рассчитываем удельные нагрузки:

а) Удельная нагрузка от собственного веса провода:

Удельная нагрузка от веса гололёда на проводе, исходя из цилиндрической формы ледяных отложений, составляет:

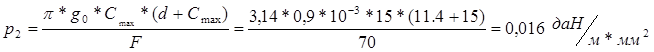
где: g₀= 0,9*10³ дaН/м³ = 0,9*10^-3 дaН/м*мм² ¾ плотность льда.

б)Суммарная удельная нагрузка от веса провода и гололёда определяется суммированием нагрузок р₁ и р₂ , так как обе эти нагрузки имеют одинаковое вертикальное направление. Отсюда,

в)Удельная нагрузка от давления ветра, действующего перпендикулярно проводу при отсутствии гололёда, составляет:

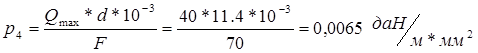
г)Удельная нагрузка при давлении ветра при наличии на проводе гололёда составляет:

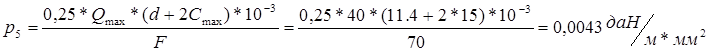
д)Удельная нагрузка от веса провода без гололёда и ветра составляет:

Удельная нагрузка от веса провода, покрытого гололёдом, и ветра составляет:

Примечание:

Удельные нагрузки р₆ и р₇ определяются геометрическим сложением составляющих, поскольку эти составляющие направлены вертикально ( р₁ и р₃ ) и горизонтально (р₄ и р₅).

Из найденных значений удельных нагрузок выбираем максимальное р_max= р₇ =0,02 даН/м*мм² , которое и будем использовать при дальнейших расчётах.

III. Определение исходного режима.

В качестве исходного режима предварительно примем режим наибольшей внешней нагрузки.

Параметры этого режима: р_max=0,02 даН/м*мм², t_г= -5^°С,

s_р.max  =[s_р.max]=11,6 даН/м*мм²

Значение температуры гололедообразования t_г= -5^°С принято в соответствии с рекомендациями, изложенными на с. 224 [1], значение допустимого механического напряжения [s_р.max] ¾ из таблицы физико-механических характеристик сталеалюминевых проводов (приложение 1 с. 85 [2])

По выражению (6.11), приведённому на с.65 [2], вычислим левую часть уравнения состояния провода:

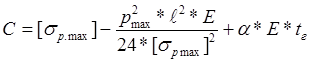, где: a-температурный коэффициент линейного удлинения материала провода. Согласно данным приложения 1 на с.85 [2] для сталеалюминевого провода марки АС сечением F=70 мм²: a=19,2*10^-6 1/^°С.

Е-модуль упругости материала провода. Согласно данным приложения 1 на с.85 [2] для сталеалюминевого провода марки АС сечением F=70мм² : Е=8,25*10³ даН/м*мм².

l—расчётная длина пролёта, м. Для предварительно принятой к установке опоры типа ПБ110-6 значение l@0,9*l_г=0,9*135=121,5 м.

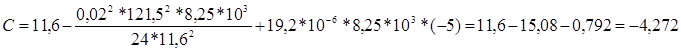
В правую часть уравнения состояния провода подставим параметры режима низшей температуры s_t.min  =[s_t.min]=11,6 даН/м*мм² (в соответствии с данными приложения 1 с.85 [2] для  сталеалюминевого провода марки АС сечением F=70мм²);р₁= 0,004даН/м*мм²; t_min = - 20^° C.

Коэффициенты А и В неполного кубического уравнения будут соответственно равны:

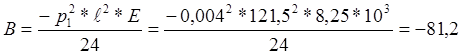
Неполное кубическое уравнение для режима низшей температуры согласно выражению (6.12) на с. 65 [2] будет иметь вид:

Решив этого уравнения (в соответствии с приложением 6 с.90 [2], при начальном приближении, приняв допустимое напряжение равным      s₀ = 11,6 даН/м*мм² ) находим величину механического напряжения в проводе в режиме низшей температуры s_t.min = 3,99 даН/м*мм².

Теперь в правую часть уравнения состояния подставим параметры режима среднегодовой температуры