




Министерство образования РФ
Санкт- Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Кафедра общей и технической физики.
ЛАБОРАТОРНАЯ РАБОТА № 4
«ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ ТОКА»
САНКТ-ПЕТЕРБУРГ
2003 г.
Цель работы – изучение магнитного поля, создаваемого током текущим по прямоугольной рамке. Измерение с помощью индукционного датчика, соединенного с ламповым вольтметром, магнитного поля Н нижнего участка этой рамки при различных расстояниях от него. Построение графика зависимости магнитного поля от расстояния и сравнение его с теоретическим, полученным на основании закона Био-Савара-Лапласа.
Общие сведения.
 Проводник, по
которому протекает электрический ток, создает магнитное поле. Магнитное поле
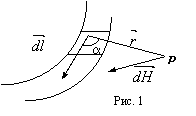
характеризуется вектором напряженности H (рис.1),
который можно вычислить по формуле
Проводник, по
которому протекает электрический ток, создает магнитное поле. Магнитное поле
характеризуется вектором напряженности H (рис.1),
который можно вычислить по формуле
H = òdH.
Cогласно закону Био-Савара-Лапласа,
![]() ,
,
где I – сила тока в проводнике, dl – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.
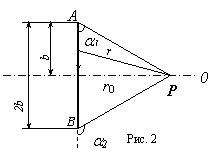 Рассмотрим
магнитное поле, создаваемое прямолинейным проводником с током конечной длины
(рис.2). Отдельные элементарные участки этого проводника создают поля dH, направленные в
одну сторону (перпендикулярно плоскости чертежа), поэтому напряженность
магнитного поля в точке P может быть найдена интегрированием:
Рассмотрим
магнитное поле, создаваемое прямолинейным проводником с током конечной длины
(рис.2). Отдельные элементарные участки этого проводника создают поля dH, направленные в
одну сторону (перпендикулярно плоскости чертежа), поэтому напряженность
магнитного поля в точке P может быть найдена интегрированием:
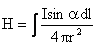
Имеем l = ro сtga, так что ![]() Кроме того,
Кроме того, ![]() Поэтому
Поэтому
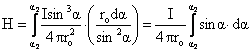
После интегрирования получим
![]() ,
(1)
,
(1)
где ro – кратчайшее расстояние от точки P до проводника с током, a1 и a2 - углы между крайними элементами проводника и соответствующими радиус-векторами PA и PB.
Если определять напряженность в точках, расположенных на перпендикуляре, восстановленном к середине проводника, то cosa2 = cos(180° -a1) = - cosa1 и, следовательно,
(cosa1 -
cosa2) =
2cosa1 = 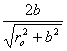 . (2)
. (2)
С учетом выражения (2) формулу (1) можно записать в виде
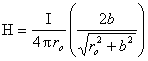 .
(3)
.
(3)
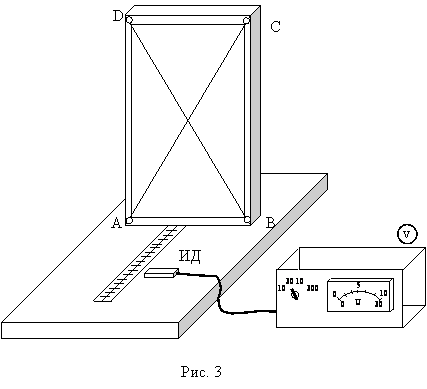 Для
исследования зависимости магнитного поля прямолинейного тока от расстояния до
проводника применяется следующий метод. Прямоугольная, вытянутая по вертикали
рамка ABCD (рис. 3) присоединяется к генератору
переменной ЭДС. По рамке течёт переменный ток, изменяющийся с течением времени t, следующим образом:
Для
исследования зависимости магнитного поля прямолинейного тока от расстояния до
проводника применяется следующий метод. Прямоугольная, вытянутая по вертикали
рамка ABCD (рис. 3) присоединяется к генератору
переменной ЭДС. По рамке течёт переменный ток, изменяющийся с течением времени t, следующим образом:
![]() ,
,
где Iо – амплитудное (максимальное) значение тока в цепи; w - угловая частота переменного тока.
Вокруг проводника создаётся переменное магнитное поле напряжённостью:
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.