Измерение напряженности магнитного поля на оси короткой катушки

Цель работы – сравнение экспериментально полученной зависимости напряженности магнитного поля на оси короткой катушки от расстояния вдоль оси H=f(z) с теоретической; определение погрешности выполненных измерений.

Общие сведения.

            Проводник, по которому протекает электрический ток, создает магнитное поле которое характеризуется вектором напряженности H (рис.1). Напряженность магнитного поля подчиняется принципу суперпозиции

а, согласно закону Био-Савара-Лапласа,

,                               (1)

где I – сила тока в проводнике, dl - вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока,   r- радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Одной из часто встречающихся конфигурации проводников с током является виток в виде кольца радиуса R (рис.2,а). Магнитное поле такого тока в плоскости, проходящей через ось симметрии, имеет вид (см. рис.2,б). Поле в целом должно иметь вращательную симметрию относительно оси z (рис.2,б), а сами силовые линии должны быть симметричны относительно плоскости петли (плоскости xy). Поле в непосредственной близости от проводника будет напоминать поле вблизи длинного прямого провода, так как здесь влияние удаленных частей петли относительно невелико. На оси кругового тока поле направлено вдоль оси Z.

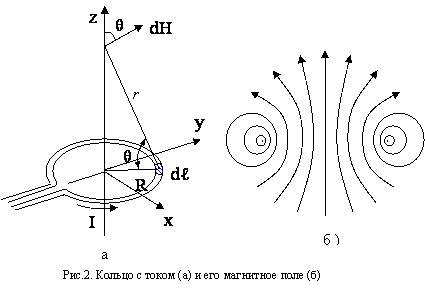
Вычислим напряженность магнитного поля на оси кольца  в точке  расположенной на расстоянии z от плоскости кольца. По формуле (1) достаточно вычислить z-компоненту вектора dH:

.                                     (2)

Интегрируя по всему кольцу, получим òdl = 2pR. Поскольку, согласно теореме Пифагора r² = R² + z², то искомое поле в точке на оси по величине равно

.                                                    (3)

Направление вектора H может быть направлено по правилу правого винта.

В центре кольца z = 0 и формула (3) упрощается .

Нас интересует короткая катушка – цилиндрическая проволочная катушка, состоящая из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси H представляет собой алгебраическую сумму полей отдельных витков H_i: . Таким образом, магнитное поле короткой катушки в произвольной точке оси рассчитывается по формуле

.                                                 (4)

Для измерения магнитного поля в данной точке используется датчик в виде катушки небольших размеров.

Если по короткой катушке пропустить изменяющийся во времени ток, то датчик будет пронизывать переменный магнитный поток Ф_H: