Вычисления значения заданной функции в заданном интервале, страница 2

Ход работы.

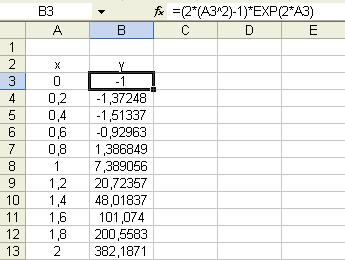
1. Вводим значения аргумента в соответствующие ячейки и высчитываем значения функции на интервале [0;2] шагом 0.2 по формуле , как это показано на рисунке 1.

Рис.1 Фрагмент окна Excel, для построения графика соответствующей функции

2. С помощью мастера диаграмм строим соответствующий график функции, используя тип диаграммы – точечная (рис.2).

Рис.2. График функции, заданной одним аналитическим выражением

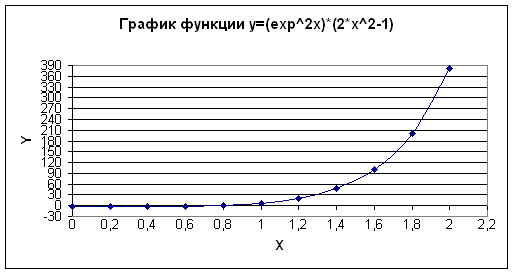
Из построенного графика, можно сделать вывод, что заданная функция монотонно возрастает при увеличении значения x и при значении аргумента, равного 2, функция принимает свое максимальное значение, а при значении аргумента 0, функция принимает минимальное значение, равное -1, что можно увидеть из рис.1.

Задание 2: Функция задана двумя аналитическими выражениями. Составить таблицу значений функции  при изменении заданной функции в интервале [-2;0.6] шагом 0.2. Вести промежуточные вычисления. Построить график функции. Распечатать отчет о работе.

Ход работы.

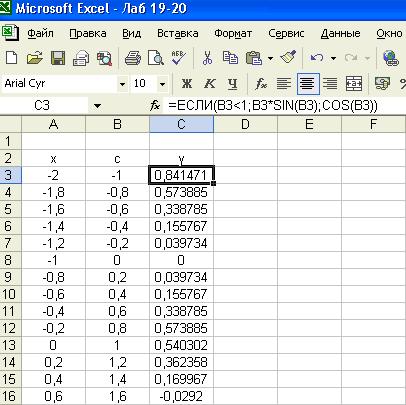
1. Составляем таблицу значений аргумента заданной функции. Сделаем замену (x+1)=c, тогда функция y примет вид:  ,а формула для расчета соответствующего значения функции при x=-2 будет иметь вид: ЕСЛИ(B3<1;B3*SIN(B3);COS(B3)). При помощи команды “копировать”, скопируем формула и для остальных значений аргумента.

Рис.3. Фрагмент окна Excel, для построения графика соответствующей функции.

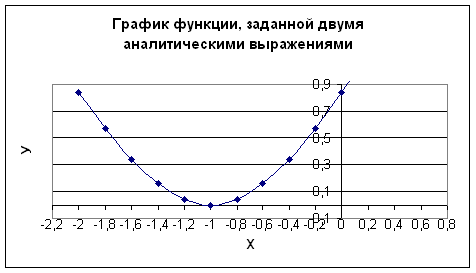
2. С помощью мастера диаграмм строим соответствующий график функции, используя тип диаграммы – точечная (рис.4).

	Рис.4 График функции, заданной двумя аналитическими выражниями

 

Из построенного графика можно сделать вывод, что заданная функция принимает свое максимальное значение в точке значения аргумента, равного 0, а наименьшее значение в точке -1.