Вычисление матричных выражений при помощи среды программирования Turbo Pascal 7.0 с использованием подпрограмм процедур, страница 2

Оглавление .

Введение……………………………………………………………………...4

1.  Теоретические сведения ………………………………………………...5

2. Постановка задачи ………………………………………………………..6

3. Анализ матричного выражения…………………………………………..7

4. Контрольный тест…………………………………………………………8

5. Программа с процедурами………………………………………………..9

6. Исходные данные………………………………………………………...11

7. Блок-схема программы…………………………………………………..12

8. Схема процедур программы…………………………………………….12

9. Программа без процедур………………………………………………...14

10. Анализ результатов расчётов…………………………………………..17

Заключение………………………………………………………………….18

Библиографический список………………………………………………..18

Введение.

Матрицы впервые были введены в математику Кэли в 1857г. Развитие современной компьютерной техники, легко выполняющей матричные операции, позволили широко использовать матрицы в различных областях знаний. Матрицы нашли особенно широкое применение в инженерных и экономических расчетах. В частности, действия с матрицами используются при решении систем линейных уравнений, в задачах, связанных с применением метода наименьших квадратов.

Вычисление матричных выражений позволяет освоить следующие действия с матрицами: сложение, вычитание матриц, умножение матриц на скаляр, транспонирование матриц, умножение 2-х матриц.

Целью выполнения расчетно-графического задания является развитие и закрепление навыков работы со средой программирования Pascal, изучаемым в курсе информатики, и применение их для самостоятельного решения, с помощью компьютера, задач из предметной области, связанной с исследованиями

1.  Теоретические сведения.

Матрица- прямоугольная таблица чисел, состоящая из строк и столбцов и рассматриваемая как единое целое. Числа, образующие матрицу, называются элементами матрицы.Число строк и столбцов в матрице называется размером матрицы. Матрица, у которой m-строки n-столбцов,называется прямоугольной матрицей размером m\n.

Матрица записывается следующим образом:

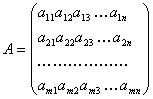
 Матричные операции бывают простые и сложные. К простым относятся сложение матриц, вычитание матриц, умножение матрицы на скаляр и транспонирование матрицы.

Сложение (вычитание матриц) определено для матриц, имеющих одинаковые размеры, и выполненяется поэлементно.

Умножение матрицы на скалярное- умножение каждого элемента матрицы на скалярное.

 Транспонирование матрицы- замена ее строк столбцами и наоборот.

 К сложным матричным операциям относят такие, как умножение двух матриц, вычисление определителя квадратной матрицы.

 Для сложных матричных операций в программе TP 7.0 предусмотрены специальные процедуры:

  MULT-(умножение двух матриц);

TR-(транспонирование матрицы).

2. Постановка задачи.

В данном расчётно-графическом задании мы будем применять технологию постепенного наращивания программы. Программа должна вводить размеры и элементы матрицы из заранее созданного файла и содержать процедуры вывода матрицы на экран, транспонирования матрицы, умножение и сложение двух матриц, а также умножение матрицы на скаляр. Сначала мы объявим все процедуры (mout, mult, slog, tr, umn), только после этого начнётся раздел операторов основной программы: введение данных из файла eist.rgz, потом преобразования над исходными матрицами и их дальнейший вывод на экран. Конечная матрица должна совпадать с матрицей посчитанной в тесте. Промежуточные матрицы тоже выводятся на экран, это делается для того, чтобы при возникновении ошибок в вычислении конечной матрицы, можно было их исправить, причём место ошибки будет сразу же видно.